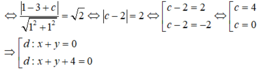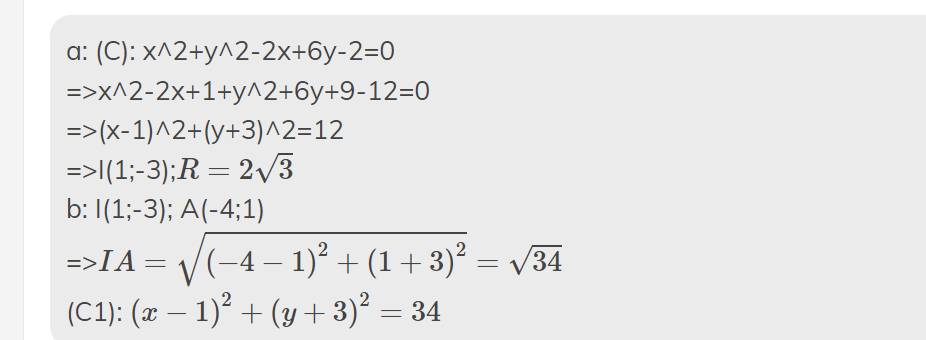PTTT: 2x+y+d=0 ( d khác -1) (d1)

do là tiếp tuyến nên 

d(I,(d1)) =R => d 

xét pt hoành độ giao điểm của d1 và (C) => tọa độ tiếp điểm 

hoặc có thể làm theo C2 

gọi H là tiếp điểm => H thuộc d1 => tọa độ tham số của H 

tính vecto IH 

có vt IH. vtcp d1 = 0 => HPTTT: 2x+y+d=0 ( d khác -1) (d1)

do là tiếp tuyến nên 

d(I,(d1)) =R => d 

xét pt hoành độ giao điểm của d1 và (C) => tọa độ tiếp điểm 

hoặc có thể làm theo C2 

gọi H là tiếp điểm => H thuộc d1 => tọa độ tham số của H 

tính vecto IH 

có vt IH. vtcp d1 = 0 => H

Phép đối xứng tâm I(1; 2) biến M(x; y) thành M’(x’; y’) thì:

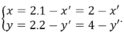
Thay vào phương trình (C) ta được:

2   -   x ' 2   +   4   -   y ' 2   +   2 ( 2   -   x '   )   -   6 ( 4   -   y '   )   +   6   =   0

⇒ x ' 2   +   y ' 2   -   6 x '   -   2 y '   +   6   =   0 hay x 2   +   y 2   -   6 x   -   2 y   +   6   =   0

Đáp án A

a) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua O.

Dùng biểu thức tọa độ của phép đối xứng qua gốc tọa độ ta có :

M′ = (2; −3), phương trình của d′: 3x – y – 9 = 0, phương trình của đường tròn (C′): x 2   +   y 2   −   2 x   +   6 y   +   6   =   0 .

b) Gọi M', d' và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua I .

Vì I là trung điểm của MM' nên M′ = (4;1)

Vì d' song song với d nên d' có phương trình 3x – y + C = 0.

Lấy một điểm trên d, chẳng hạn N(0; 9).

Khi đó ảnh của N qua phép đối xứng qua tâm I là N′(2; −5).

Vì N' thuộc d nên ta có 3.2 − (−5) + C = 0. Từ đó suy ra C = -11.

Vậy phương trình của d' là 3x – y – 11 = 0.

Để tìm (C'), trước hết ta để ý rằng (C) là đường tròn tâm J(−1; 3),

bán kính bằng 2. Ảnh của J qua phép đối xứng qua tâm I là J′(3; 1).

Do đó (C') là đường tròn tâm J' bán kính bằng 2. Phương trình của (C') là x   −   3 2   +   y   −   1 2   =   4 .

a) Để tìm tọa độ tâm và bán kính của đường tròn ©, ta cần viết lại phương trình của nó dưới dạng chuẩn:
\begin{align*}
x^2 + y^2 - 2x + 6y - 2 &= 0 \
\Leftrightarrow (x-1)^2 + (y+3)^2 &= 14
\end{align*}
Vậy, tọa độ tâm của đường tròn © là $(1,-3)$ và bán kính của đường tròn © là $\sqrt{14}$.

b) Đường tròn có tâm $I(4,3)$ và đi qua $A(-4,1)$ có phương trình là:
$$(x-4)^2 + (y-3)^2 = (-4-4)^2 + (1-3)^2 = 20$$

c) Để tìm phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d: 3x+4y-4=0$ tại hai điểm $M$ và $N$ sao cho $MN=6$, ta có thể làm như sau:

Tìm giao điểm $H$ của đường thẳng $d$ và đường vuông góc với $d$ đi qua $I$.Tìm hai điểm $M$ và $N$ trên đường thẳng $d$ sao cho $HM=HN=3$.Xây dựng đường tròn (C') có tâm là $I$ và bán kính bằng $IN=IM=\sqrt{3^2+4^2}=5$.

Để tìm giao điểm $H$, ta cần tìm phương trình của đường thẳng vuông góc với $d$ đi qua $I$. Đường thẳng đó có phương trình là:
$$4x - 3y - 7 = 0$$
Giao điểm $H$ của đường thẳng này và $d$ có tọa độ là $(\frac{52}{25}, \frac{9}{25})$.

Để tìm hai điểm $M$ và $N$, ta có thể sử dụng công thức khoảng cách giữa điểm và đường thẳng. Khoảng cách từ điểm $H$ đến đường thẳng $d$ là:
$$d(H,d) = \frac{|3\cdot \frac{52}{25} + 4\cdot \frac{9}{25} - 4|}{\sqrt{3^2+4^2}} = \frac{1}{5}$$
Vậy, hai điểm $M$ và $N$ cách $H$ một khoảng bằng $\frac{3}{5}$ và $\frac{4}{5}$ đơn vị theo hướng vuông góc với $d$. Ta có thể tính được tọa độ của $M$ và $N$ như sau:
$$M = \left(\frac{52}{25} - \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{3}{5}\cdot 3\right) = \left(\frac{12}{25}, \frac{54}{25}\right)$$
và
$$N = \left(\frac{52}{25} + \frac{4}{5}\cdot 4, \frac{9}{25} + \frac{4}{5}\cdot 3\right) = \left(\frac{92}{25}, \frac{27}{5}\right)$$
Cuối cùng, phương trình đường tròn (C') có tâm là $I(4,3)$ và cắt đường thẳng $d$ tại hai điểm $M$ và $N$ sao cho $MN=6$ là:
$$(x-4)^2 + (y-3)^2 = 5^2$$

Tên quen ta :))

Lời giải:

Tiếp tuyến $(d')$ cần tìm song song với $(d): x+y-3=0$ nên có dạng $x+y+m=0$

Viết lại PTĐTr $(C): (x-1)^2+(y+2)^2=8$

$\Rightarrow$ tâm $I(1;-2)$ và bán kính $R=2\sqrt{2}$

Vì $(d')$ là tiếp tuyến của $(C)$ nên: \(d(I, d')=R\Leftrightarrow \frac{|x_I+y_I+m|}{\sqrt{1^2+1^2}}=2\sqrt{2}\)

\(\Leftrightarrow |m-1|=4\Rightarrow m=5\) hoặc $m=-3$. TH $m=-3$ loại do trùng với $(d)$

Vậy PTTT cần tìm là $x+y+5=0$

Đáp án: B

(C): x 2  + y 2  - 2x + 6y + 8 = 0

⇔ (x - 1 ) 2  + (y + 3 ) 2  = 2 có I(1;-3), R = 2

Gọi d’ là tiếp tuyến của đường tròn (C) và song song với d

Vì d'//d ⇒ d': x + y + c = 0, (c ≠ 4)

d’ là tiếp tuyến của (C) nên d(I;d') = R