Tìm một số tự nhiên có 4 chữ số,biết rằng nếu xóa đi 2 chứ số cuối thì được số mới bé hơn số ban đầu là 1496 đơn vị.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


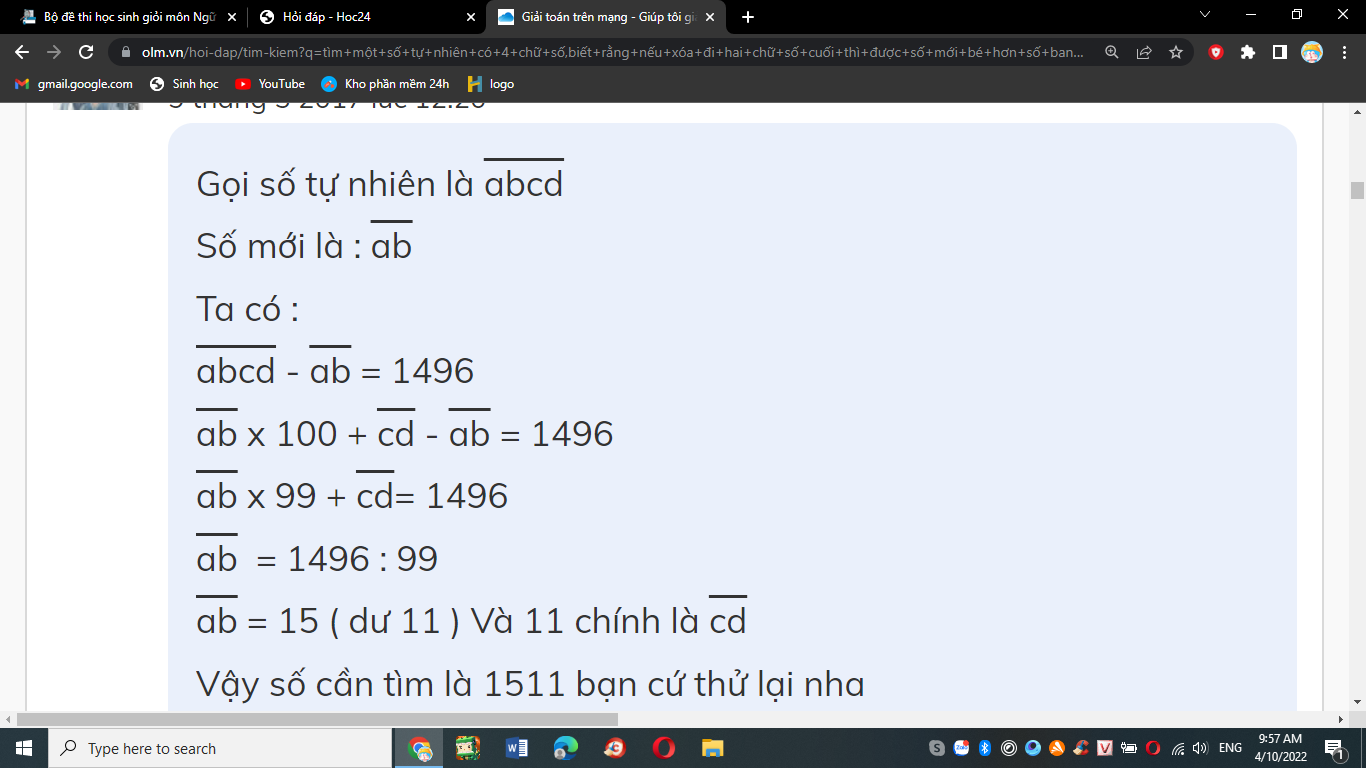
Gọi số tự nhiên là abcd
Số mới là : ab
Ta có :
abcd - ab = 1496
ab x 100 + cd - ab = 1496
ab x 99 + cd= 1496
ab = 1496 : 99
ab = 15 ( dư 11 ) Và 11 chính là cd
Vậy số cần tìm là 1511 bạn cứ thử lại nha

Gọi số tự nhiên là : abcd
Số mới là : ab
Ta có:
abcd - ab = 1496
ab x 100 + cd - ab = 1496
ab x 99 + cd = 1496
ab = 1496: 99
ab =15(dư 11)và 11 chính là cd
Vậy số cần tìm là 1511.
Gọi số tự nhiên là abcd
Số mới là : ab
Ta có :
abcd - ab = 1496
ab x 100 + cd - ab = 1496
ab x 99 + cd= 1496
ab = 1496 : 99
ab = 15 ( dư 11 ) Và 11 chính là cd
Vậy số cần tìm là 1511 bạn cứ thử lại nha

tham khảo
Gọi số tự nhiên là abcd
Số mới là : ab
Ta có :
abcd - ab = 1496
ab x 100 + cd - ab = 1496
ab x 99 + cd= 1496
ab = 1496 : 99
ab = 15 ( dư 11 ) Và 11 chính là cd
Vậy số cần tìm là 1511
tham khảo
Gọi số tự nhiên là abcd
Số mới là : ab
Ta có :
abcd - ab = 1496
ab x 100 + cd - ab = 1496
ab x 99 + cd= 1496
ab = 1496 : 99
ab = 15 ( dư 11 ) Và 11 chính là cd
Vậy số cần tìm là 1511

Gọi số tự nhiên là abcd
Số mới là : ab
Ta có :
abcd - ab = 1496
ab x 100 + cd - ab = 1496
ab x 99 + cd= 1496
ab = 1496 : 99
ab = 15 ( dư 11 ) Và 11 chính là cd
Vậy số cần tìm là 1511 bạn cứ thử lại nha
Gọi số tự nhiên là abcd
Số mới là : ab
Ta có :
abcd - ab = 1496
ab x 100 + cd - ab = 1496
ab x 99 + cd= 1496
ab = 1496 : 99
ab = 15 ( dư 11 ) Và 11 chính là cd
Vậy số cần tìm là 1511 bạn cứ thử lại nha

Ta gọi số tự nhiên cần tìm là abcd, 2 chữ số đã xóa là cd, ta có:
abcd - ab = 2688
abcd x 100 + cd - ab = 2688
(ab x 100 - ab) + cd = 2688
(ab x 100 - ab x 1) + cd = 2688
ab x (100 - 1) + cd = 2688
ab x 99 + cd = 2688
=> 2688 : 99 = ab (dư cd)
Mà 2688 : 99 = 27 (dư 15). Vậy số tự nhiên cần tìm là 2715.
Đáp số: 2715

Gọi số cần tìm là \(\overline{abcd}\) với a, b, c, d là các chữ số và a khác 0.
Khi xóa hai chữ số cuối thì ta được số \(\overline{ab}\)
Theo đề bài ta có: \(\overline{abcd}-\overline{ab}=1496\)
Do \(10< \overline{ab}< 100\) nên \(1506< \overline{abcd}< 1595\)
\(\Rightarrow\overline{ab}=15\)
Vậy thì \(\overline{15cd}-15=1496\)
\(1500+\overline{cd}=1511\)
\(\overline{cd}=11\)
Vậy số cần tìm là 1511.
Nếu xóa đi 2 số cuối của số tự nhiên 4 chữ số ta nhận được số tự nhiên mới là hai chữ số đầu tiên của số ban đầu mà số mới bé hơn số ban đầu 1496 đơn vị
Nên Hai chữ số đó chỉ có thể là 14 hoặc 15
Nếu số mới là: 14 thì số ban đầu là: 1496 +14=1510 ( loại )
Nếu số mới là: 15 thì số ban đầu là: 1496 + 15 = 1511 Thỏa mãn.
Vậy số cần tìm là 1511