a: Xét ΔABC có 

\(\widehat{A}+\widehat{ABC}+\widehat{ACB}=180^0\)

\(\Leftrightarrow2\cdot\left(\widehat{IBC}+\widehat{ICB}\right)=180^0-60^0=120^0\)

\(\Leftrightarrow\widehat{IBC}+\widehat{ICB}=60^0\)

\(\Leftrightarrow\widehat{BIC}=120^0\)

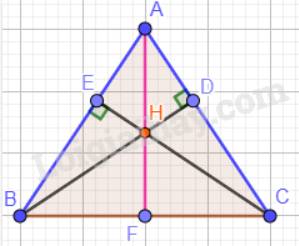
a) Tam giác ABC cân tại A nên: \(\widehat {ABC} = \widehat {ACB} = 70^\circ \).

Tổng ba góc trong một tam giác bằng 180° nên: \(\widehat {BAC} = 180^\circ  - 70^\circ  - 70^\circ  = 40^\circ \).

b) Xét tam giác vuông ADB và tam giác vuông AEC có:

     AB = AC (tam giác ABC cân);

     \(\widehat A\) chung.

Vậy \(\Delta ADB = \Delta AEC\)(cạnh huyền – góc nhọn). Suy ra: BD = CE ( 2 cạnh tương ứng).

c) Trong tam giác ABC có H là giao điểm của hai đường cao BD và CE nên H là trực tâm trong tam giác ABC hay AF vuông góc với BC.

Xét hai tam giác vuông AFB và AFC có:

     AB = AC (tam giác ABC cân);

     AF chung.

Vậy \(\Delta AFB = \Delta AFC\)(cạnh huyền – cạnh góc vuông). Suy ra: \(\widehat {FAB} = \widehat {FAC}\) ( 2 góc tương ứng) hay \(\widehat {BAH} = \widehat {CAH}\).

Vậy tia AH là tia phân giác của góc BAC.

Trong tam giác ABC có : ABC + ACB + BAC = 180 => ABC + ACB = 120 

mà BD , CE lần lượt là phân giác của ABC , ACB => 2IBC + 2ICB = 120 <=> IBC + ICB = 60 

Có : DIE+DIC = 180 ( kề bù ) mà DIC = IBC + ICB = 60 ( góc ngoài của tam giác IBC ) 

=> DIE = 120 và DIE + BAC = 180 => AEID nội tiếp

Mình đến trễ mong bạn thông cảm lời giải đây ạ

a, 

ta có 

A + B+ C = \(180^0\)

B + C  = \(180^0\)-  A

mà BI là phân giác góc B

IBC = \(\frac{1}{2}\)B

CI là phân giác góc C 

ICB = \(\frac{1}{2}\)C

suy ra 

IBC + ICB = \(\frac{1}{2}\)B + \(\frac{1}{2}\)C = \(\frac{1}{2}\)( B + C ) = \(\frac{1}{2}\)( \(180^0\)- A ) = \(\frac{1}{2}\) \(\left(180^0-60^0\right)\)= \(60^0\)

mà IBC + ICB + BIC = \(180^0\)

suy ra BIC = \(180^0\)- ( IBC + ICB )

          BIC = \(180^0\)- \(60^0\) 

          BIC = \(120^0\)

b,

ta có vì I là giao điểm của phân giác góc B và C 

suy ra phân giác góc A đi qua I suy ra tia AI trùng tia IF suy ra AF là phần giác góc A mà I cách đều AB ; AC ; BC 

nên IE = ID = IF

c,

ta có EIB + BIC =\(180^0\) 

       EIB = \(180^0-120^0\)

     EIB = \(60^0\)

    Mà EIB đối đỉnh góc DIC 

suy ra DIC = EIB =  \(60^0\)

vì IF là tia phân giác góc BIC 

nên BIF = CIF = \(\frac{1}{2}\)\(120^0\)= \(60^0\)

EIF = BIE + BIF = \(60^0+60^0=120^0\)

DIF = DIC + CIF =  \(60^0+60^0=120^0\)

xét tam giác EIF và DIF có 

EIF = DIF = \(120^0\)

IF là cạnh chung 

IE = ID 

suy ra tam giác EIF = tam giác DIF ( c-g-c )

suy ra EF = DF 

ta có góc BIC đối đỉnh góc EID 

nên BIC = EID = \(120^0\)

xét tam giác EIF và EID có 

EID = EIF =\(120^0\)

ID = IF 

IE cạnh chung 

suy ra tam giác DIE = tam giác FIE ( c-g-c )

suy ra ED = EF 

mà EF = DF 

suy ra ED = EF = DF

suy ra tam giác EDF là tam giác đều 

d,

ta có IE = IF = ID 

nên I cách đều 3 đỉnh tam giác DFE nên I là giao điểm của 3 đường trung trực tam giác DEF 

mà trong tam giác đều 3 đường trung trực đồng thời là 3 đường phân giác của tam giác đó 

suy ra I là giao điểm của hai đường phân giác trong tam giác ABC vá DEF

a) Ta thấy \(\widehat{B}+\widehat{C}=180^o-60^o=120^o\)

\(\Rightarrow\widehat{IBC}+\widehat{ICB}=\frac{\widehat{B}+\widehat{C}}{2}=60^o\)

Vậy thì \(\widehat{BIC}=180^o-\widehat{IBC}-\widehat{ICB}=120^o\)

b) Ta có ngay \(\widehat{EIB}=\widehat{IBC}+\widehat{ICB}=60^o=\widehat{BIN}\)

Vậy thì \(\Delta EBI=\Delta NBI\left(g-c-g\right)\Rightarrow IE=IN\)

Tương tự ID = IN nên IE = IN = ID.

a, Trong tam giác ABC có : góc ABC + góc ACB + góc BAC = 180 độ
=> góc ABC + góc ACB  =180 độ - góc BAC = 180 độ - 60 độ = 120 độ
Mà BD và CE lần lượt là phân giác của góc ABC ; ACB nên 
120 độ = 2.góc IBC + 2.góc ICB = 2.(góc IBC + góc ICB)
=> góc IBC + góc ICB = 120 độ : 2 = 60 độ
Trong tam giác IBC có : góc IBC + góc ICB + góc BIC = 180 độ
=> góc BIC = 180 độ - (góc IBC + góc ICB) = 180 độ - 60 độ = 120 độ

haha

chẳg aj tl âu

bt oy , 0 cần ns âu