Cho đa thức B(x) = 1 + x + x2 + x3 + ...+ x99 + x100 . Tính giá trị của đa thức B(x) tại x=1/2
Mong các bạn giúp đỡ !
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 3 2021
a)\(A=1+x+x^2+x^3+..........+x^{2012}\)
+)Thay x=1 vào biểu thức đc:
\(A=1+1+1^2+1^3+..............+1^{2012}\)
Có 2013 số hạng
\(\Rightarrow A=1.2013=2013\)
b)\(B=1-x+x^2-x^3+..............-x^{2011}\)
\(\Rightarrow B=\left(1-x\right)+\left(x^2-x^3\right)+............+\left(x^{2010}-x^{2011}\right)\)
+)Thay x=1 vào biểu thức được:
\(B=\left(1-1\right)+\left(1^2-1^3\right)+...........+\left(1^{2010}-1^{2011}\right)\)
\(\Rightarrow B=0+0+......................+0=0\)
+)\(C=A+B\Rightarrow C=2013+0\Rightarrow C=2013\)
Vậy C=2013
Chúc bn học tốt
28 tháng 7 2023
A(x)=F(x)-G(x)
=1+x+x^2+...+x^100-x^2-x^4-...-x^100
=1+x+x^3+...+x^99
Số số lẻ từ 1 đến 99 là (99-1):2+1=50(số)
A(-1)=1+(-1)+(-1)^3+...+(-1)^99
=1-50*1=1-50=-49
PT
1
CM
10 tháng 1 2017
Thay x = -1 và đa thức, ta có:
(-1)2 + (-1)4 + (-1)6 + … + (-1)100 =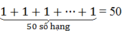 
Vậy giá trị đa thức bằng 50 tại x = -1.
7 tháng 5 2023
a. Thay x = 1 vào đa thức ta có:
\(1^2-4.1+4=1\)
Thay x = 2 vào đa thức ta có
\(2^2-4.2+4=0\)
Thay x = 3 vào đa thức ta có:
\(3^2-4.3+4=1\)
Thay x = -1 vào đa thức ta có:
\(\left(-1\right)^2-4.\left(-1\right)+4=9\)
b. Trong các số trên 2 là nghiệm của đa thức M(x)
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
7 tháng 5 2023
a, M(\(x\)) = \(x^2\) - 4\(x\) + 4
M(1) = 12 - 4.1 + 4 = 1
M(2) = 22 - 4.2 + 4 = 0
M(3) = 32 - 4.3 + 4 = 1
M(-1) = (-1)2 - 4.(-1) + 4 = 9
b, Trong các số 1; 2; 3 và -1 thì 2 là nghiệm của M(\(x\)) vì M(2) = 0
T
27 tháng 10 2023
a,
\(A=4(x-2)(x+1)+(2x-4)^2+(x+1)^2\\=[2(x-2)]^2+2\cdot2(x-2)(x+1)+(x+1)^2\\=[2(x-2)+(x+1)]^2\\=(2x-4+x+1)^2\\=(3x-3)^2\)
Thay $x=\dfrac12$ vào $A$, ta được:
\(A=\Bigg(3\cdot\dfrac12-3\Bigg)^2=\Bigg(\dfrac{-3}{2}\Bigg)^2=\dfrac94\)
Vậy $A=\dfrac94$ khi $x=\dfrac12$.
b,
\(B=x^9-x^7-x^6-x^5+x^4+x^3+x^2-1\\=(x^9-1)-(x^7-x^4)-(x^6-x^3)-(x^5-x^2)\\=[(x^3)^3-1]-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1)-x^4(x^3-1)-x^3(x^3-1)-x^2(x^3-1)\\=(x^3-1)(x^6+x^3+1-x^4-x^3-x^2)\\=(x^3-1)(x^6-x^4-x^2+1)\)
Thay $x=1$ vào $B$, ta được:
\(B=(1^3-1)(1^6-1^4-1^2+1)=0\)
Vậy $B=0$ khi $x=1$.
$Toru$