â, Vì D đối xứng với M qua AB ⇒ AD=AM ⇒ ΔADM cân tại A ⇒ ∠A1= ∠A2=1/2 ∠DAM ⇒ ∠DAM=2 ∠A2

Vì E đối xứng với M qua AC ⇒ AE=ÂM ⇒ ΔAEM cân tại A ⇒ ∠A3= ∠A4=1/2 ∠AEM ⇒ ∠AEM=2 ∠A3

⇒ ∠DAE= ∠DAM+ ∠MAE

=2 lần góc A2+ 2 lần góc A3

=2(góc A2+A3)

= 2 lần góc BAC

= 2.70=140

Xét ΔDAE có AD=AE(=ÂM) ⇒ ΔDAE cân tại A

⇒ ∠ADE= ∠AED=180- ∠DAE/2=180-140/2=40/2=20

b, Xét ΔADI và ΔAMI có:

AD=AM(cmt)

∠A1= ∠A2

ẠI chúng

⇒ΔADI = ΔAMI(c.g.c)

⇒ ∠ADI= ∠AMI( 2 góc t/u) (1)

Xét ΔAMK và ΔAEK có:

ÂM=AE(cmt)

∠A3= ∠A4

AK chúng

⇒ΔAMK = ΔAEK(c.g.c)

⇒ ∠AMK= ∠AEK( 2 góc t/u) (2)

mà góc ADE= AED (3)

Từ (1),(2),(3) ⇒ ∠AMI= ∠AMK ⇒AM là tia phân giác ∠IMK

c, Để DE ngắn nhất ⇔ ΔADE cân tại A có AD=AE ngắn nhất

má AD=AE=AM(cmt) ⇔AM ngắn nhất

Kẻ AH vuông góc BC ⇒ ΔAHM vuông tại H ⇒AH ≤AM

AM ngắn nhất ⇔AM=AH ⇔ ∠M= ∠H

dấu ∠ có nghĩa là j z bn

a: Ta có: E và D đối xứng nhau qua AB

nên AB là đường trung trực của ED

Suy ra: AB\(\perp\)ED tại I và I là trung điểm của ED

Xét ΔAEI vuông tại I và ΔADI vuông tại I có 

AI chung

EI=DI

Do đó: ΔAEI=ΔADI

Bạn xem ở đây nhé

Câu hỏi của Nguyễn Thị Thùy - Toán lớp 8 - Học toán với OnlineMath

Bài 2 : c/m là AB+AC<BM+MC nha mấy bạn giúp mk vs 

Tham khảo:

Ta có: \(\widehat{DAB}=\widehat{MAB}\) , \(\widehat{EAC}=\widehat{MAC}\) (do tính chất đối xứng)

=> \(\widehat{DAE}=2.\widehat{BAC}\) là đại lượng không đổi khi M di chuyển trên BC.

=> \(DE^2=AD^2+AE^2-2.AD.AE.\cos\widehat{DAE}\)

Mà AD = AE = AM

=> \(DE^2=AM^2+AM^2-2.AM.AM.\cos\left(2.\widehat{BAC}\right)\)

               \(=2.AM^2\left[1-\cos2\widehat{BAC}\right]\)

=> DE nhỏ nhất khi AM nhỏ nhất => M là chân đường cao hạ từ A xuống BC

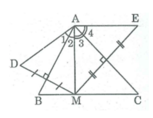
Vì D đối xứng với M qua trục AB

⇒ AB là đường trung trực của MD.

⇒ AD = AM (t/chất đường trung trực) (1)

Vì E đối xứng với M qua trục AC

⇒ AC là đường trung trực của ME

⇒ AM = AE (t/chất đường trung trực) (2)

Từ (1) và (2) suy ra: AD = AE

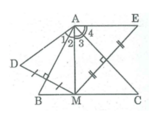
AD = AM suy ra ∆ AMD cân tại A có AB ⊥ MD nên AB cũng là đường phân giác của ∠ (MAD)

⇒ ∠ A 1 =  ∠ A 2

AM = AE suy ra  ∆ AME cân tại A có AC ⊥ ME nên AC cũng là đường phân giác của  ∠ (MAE)

⇒  ∠ A 3  =  ∠ A 4

∠ (DAE) =  ∠ A 1  +  ∠ A 2  +  ∠ A 3  +  ∠ A 4  = 2(  ∠ A 2 +  ∠ A 3  ) = 2 ∠ (BAC) = 2. 70 0  =  140 0