Câu 5: Một người đi xe đạp đi nửa quãng đường đầu với vận tốc 10 km/h nửa quãng đường sau đi với vận tốc 20 km/h tính vận tốc trung bình trên cả quãng đường.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi S(km) là độ dài quãng đường (S>0)
\(\left\{{}\begin{matrix}t_1=\dfrac{\dfrac{S}{2}}{v_1}=\dfrac{S}{2.4}=\dfrac{S}{8}\left(h\right)\\t_2=\dfrac{\dfrac{S}{2}}{v_2}=\dfrac{S}{2.6}=\dfrac{S}{12}\left(h\right)\end{matrix}\right.\)
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{8}+\dfrac{S}{12}}=\dfrac{S}{\dfrac{5}{24}S}=\dfrac{24}{5}=4,8\left(km/h\right)\)

Gọi nửa QĐ là S
vtb = 2s/(s/v1+s/v2) = 2/(1/12+1/20) = 15km/h

Gọi s là chiều dài nửa quãng đường mà người đi xe đạp phải đi.
Như vậy, thời gian đi hết nửa quãng đường đầu s1 = s với vận tốc v1 là:
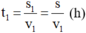
Thời gian đi hết nửa quãng đường còn lại s2 = s với vận tốc v2 là:
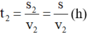
Vậy tổng thời gian đi hết cả quãng đường là: 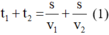
Vận tốc trung bình của người đi xe đạp trên cả quãng đường là:
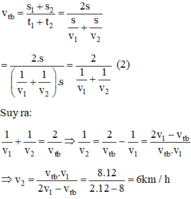

\(v_{tb}=\dfrac{s}{\dfrac{\dfrac{1}{2}s}{v'}+\dfrac{\dfrac{1}{2}s}{v''}}=\dfrac{s}{\dfrac{s}{20}+\dfrac{s}{15}}=\dfrac{s}{\dfrac{7s}{60}}=\dfrac{60}{7}\approx8,6\left(\dfrac{km}{h}\right)\)
Thời gian xe đi nửa quãng đường đầu:
\(t_1=\dfrac{S_1}{v_1}=\dfrac{\dfrac{S}{2}}{v_1}=\dfrac{S}{2v_1}=\dfrac{S}{2\cdot20}=\dfrac{S}{40}\left(h\right)\)
Thời gian xe đi trên nửa quãng đường sau:
\(t_2=\dfrac{S_2}{v_2}=\dfrac{\dfrac{S}{2}}{v_2}=\dfrac{S}{2v_2}=\dfrac{S}{2\cdot15}=\dfrac{S}{30}\left(h\right)\)
Vận tốc trung bình trên cả quãng đường:
\(v_{tb}=\dfrac{S_1+S_2}{t_1+t_2}=\dfrac{S}{\dfrac{S}{40}+\dfrac{S}{30}}=\dfrac{S}{\dfrac{7S}{120}}=\dfrac{120}{7}\approx17,14\)km/h
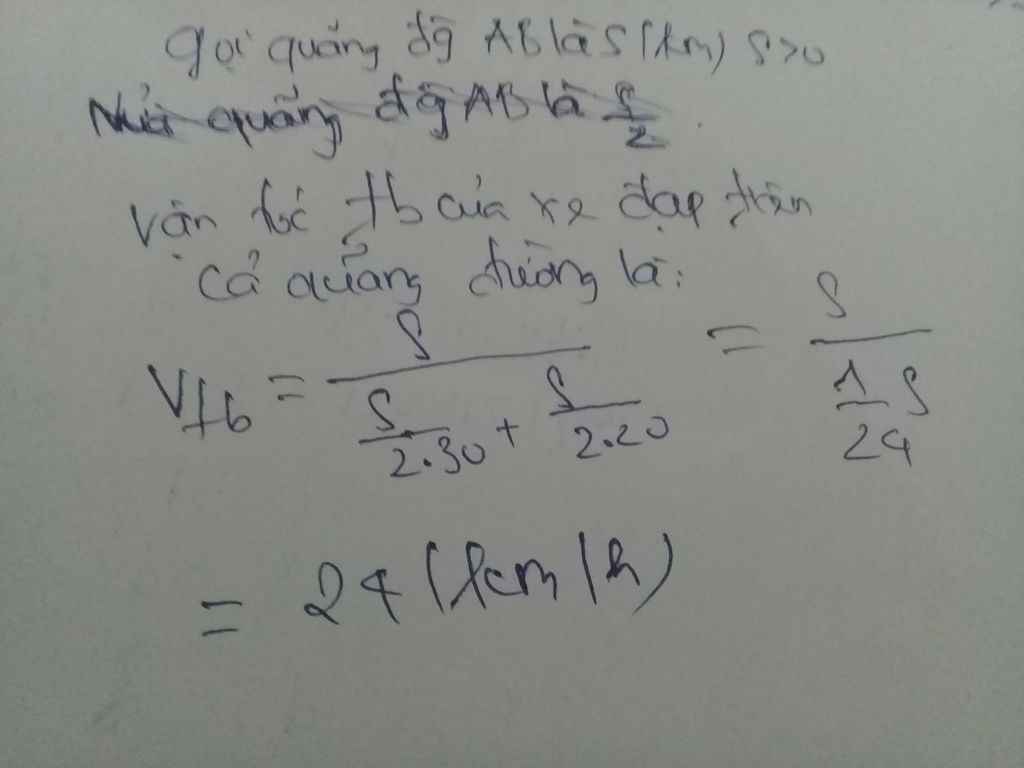
<Bạn tự tóm tắt>
Vận tốc trung bình của xe là: \( v=\dfrac{s}{\dfrac{s}{2}(\dfrac{1}{v_1}+\dfrac{1}{v_2})} =\dfrac{1}{\dfrac{1}{2}(\dfrac{1}{ 10 }+\dfrac{1}{ 20 })} =\dfrac{40}{3}(km/h)\)