giúp mình b,c,d với ạ
Bài 5:. Cho tam giác ABC vuông tại A có M, N, P lần lượt là trung điểm BC, AB, AC.
a) Chứng minh BNPC là hình thang;
b) Tứ giác ANMP là hình gì? Vì sao?
c) Gọi D đối xứng với M qua N, E đối xứng với M qua P. CM: D, A, E thẳng hàng;
d) Để tam giác MED là tam giác vuông cân thì tam giác ABC cần thêm điều kiện gì?

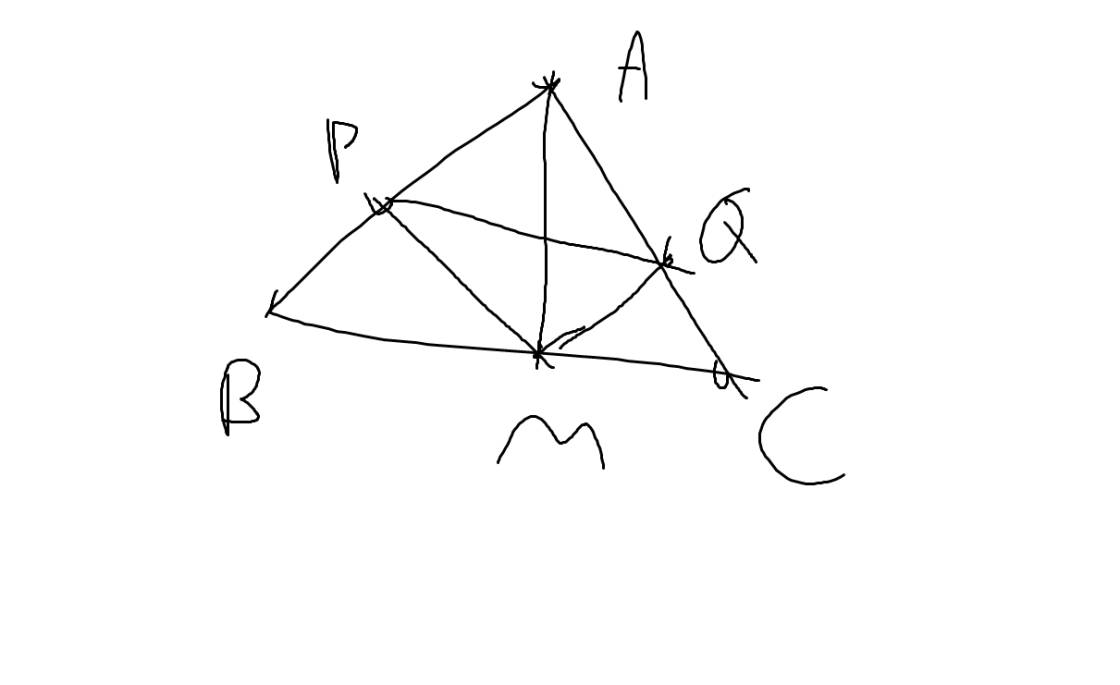
a: Xét ΔABC có
N là trung điểm của AB
P là trung điểm của AC
Do đó: NP là đường trung bình của ΔBAC
Suy ra: NP//BC
hay BNPC là hình thang
giúp mình b,c,d với ạ