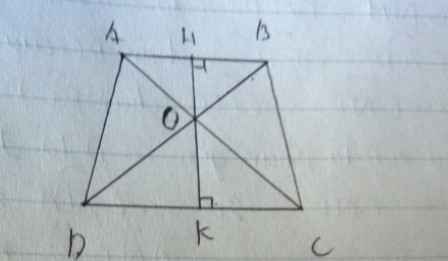
Cho hình thang ABCD (như hình vẽ). Hãy so sánh diện tích của hình tam giác ACD vớiBCD, diện tích của hình tam giác AOD với BOC.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Vì AB//CD
nên \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
Ta có: \(\dfrac{S_{BOA}}{S_{BOC}}=\dfrac{OA}{OC}\)
\(\dfrac{S_{BOA}}{S_{AOD}}=\dfrac{OB}{OD}\)
mà \(\dfrac{OA}{OC}=\dfrac{OB}{OD}\)
nên \(S_{BOC}=S_{AOD}\)

\(ABssCD\Rightarrow\dfrac{AB}{CD}=\dfrac{OB}{OD}=\dfrac{OA}{OC}=\dfrac{2}{3}\)
a)\(S_{AOD}=\dfrac{1}{2}OA.OD.sinAOB\)
\(S_{BOC}=\dfrac{1}{2}OB.OC.sinBOC\)
\(\Rightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{OA.OD}{OB.OC}\) vì \(\widehat{AOD}=\widehat{BOC}\Rightarrow sinAOD=sinBOC\)
\(\Leftrightarrow\dfrac{S_{AOD}}{S_{BOC}}=\dfrac{2}{3}.\dfrac{3}{2}=1\)
b) vì \(ABssCD\Rightarrow\dfrac{OH}{OK}=\dfrac{2}{3}\Rightarrow\dfrac{OH}{HK}=\dfrac{2}{5}\)
\(S_{AOB}=\dfrac{1}{2}.OH.AB\\ S_{ABCD}=\dfrac{1}{2}\left(AB+CD\right).HK=\dfrac{1}{2}\left(AB+\dfrac{3}{2}AB\right).HK=\dfrac{1}{2}.\dfrac{5}{2}AB.HK\)
\(\Rightarrow\dfrac{S_{AOB}}{S_{ABCD}}=\dfrac{\dfrac{1}{2}OH.AB}{\dfrac{1}{2}HK.\dfrac{5}{2}AB}=\dfrac{2}{5}.\dfrac{1}{\dfrac{5}{2}}=\dfrac{4}{25}\)
\(\Rightarrow S_{ABCD}=\dfrac{4}{\dfrac{4}{25}}=25\)

Bài giải dài lắm xin lỗi bạn nha. Nếu được thì cho mình địa chỉ mail nhé. Mình gửi lời giải cho

a: Xét ΔOBA và ΔODC có
góc OBA=góc ODC
góc BOA=góc DOC
=>ΔOBA đồng dạng với ΔODC
=>OB/OD=OA/OC=AB/CD=1/3
=>S ABO=1/3*S ABC
=>S BOC=2/3*S ABC
b: Kẻ CH vuông góc AB
=>S ABC=1/2*CH*AB
S ABCD=1/2*CH*(AB+CD)
=>S ABC/S ABCD=AB/(AB+CD)
Giải
Tam giác ACD và BCD có đáy bằng nhau, chiều cao bằng nhau
=> \(S_{ACD}=S_{BCD}\)
Còn AOD với BOC....
Cho tớ hỏi: Điểm O LẠC TRÔI ĐI ĐÂU RỒI ?!?!?!?!
nằm ở chỗ 2 đường thẳng AD và BC cắt nhau đó bạn :)