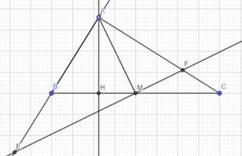
1,Cho tam giác ABC vuông tại A có đường cao AH, trung tuyến AM. Qua H kẻ đường thẳng // AB cắt AC tại D, kẻ đường thẳng // AC vắt AB tại E . Chứng minh:
a, AH=DE
b,BAM vuông góc với DE
c, tam giác ABC cần thêm điều kiện gì để AEHD là hình vuông
a Cho AB=6,AC=8. Tính SAEMD
2,Cho ABCD là hcn có O là giao điểm của 2 đường chéo.Trên OB lấy I.Gọi E là điểm đối xứng với A qua I.
a,C/M OIEC là hình thang
b, Gọi K là trung điểm của CE.C/M IK=OC
c, Đường thẳng IK cắt BC tại F và cắt DC tại H,C/M tam giác KHC cân
d, Tứ giác ABCD cần thêm điều kiện gì để OIKC là hcn
3, Cho tam giác ABC có góc A=90độ, AB<AC,trung tuyến AM.Vẽ tia Mx//AB cắt AC tại H.Trên tia Mx lấy điểm K sao cho MK=AB
a,C/M BM=AK
b,C/M M,K đx với nhau qua AC
c, Từ C vẽ đường thẳng vuông góc với AC cắt AM tại Q.C/M ACQB là hcn