CMR biểu thức A=75.(4^2017+4^2016+..+4^2+5)+25 chia hết cho 4^2018
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NQ
0
12 tháng 5 2022
Đặt \(D=1+4+...+4^{2019}\)
\(\Leftrightarrow4D=4+4^2+...+4^{2020}\)
\(\Leftrightarrow D=\dfrac{4^{2020}-1}{3}\)
\(C=75\cdot D+25\)
\(=25\left(4^{2020}-1\right)+25=25\cdot4\cdot4^{2019}⋮100\)
NM
1
TT
1
22 tháng 12 2017
đặt B = 42015 + 42014 + 42013 + ... + 42
4B = 42016 + 42015 + 42014 + ... + 43
4B - B = ( 42016 + 42015 + 42014 + ... + 43 ) - ( 42015 + 42014 + 42013 + ... + 42 )
3B = 42016 - 42
\(\Rightarrow\)B = \(\frac{4^{2016}-4^2}{3}\)hay B = \(\frac{4^{2016}-16}{3}\)
\(\Rightarrow\)A = 75 . ( \(\frac{4^{2016}-16}{3}\)+ 5 ) + 25
A = 75 . ( \(\frac{4^{2016}-16}{3}\)+ \(\frac{15}{3}\)) + 25
A = 75 . ( \(\frac{4^{2016}-1}{3}\)) + 25
A = 25 . ( 3 . \(\frac{4^{2016}-1}{3}\)) + 25
A = 25 . ( 42016 - 1 ) + 25
A = 25 . ( 42016 - 1 + 1 )
A = 25 . 42016 \(⋮\)42016
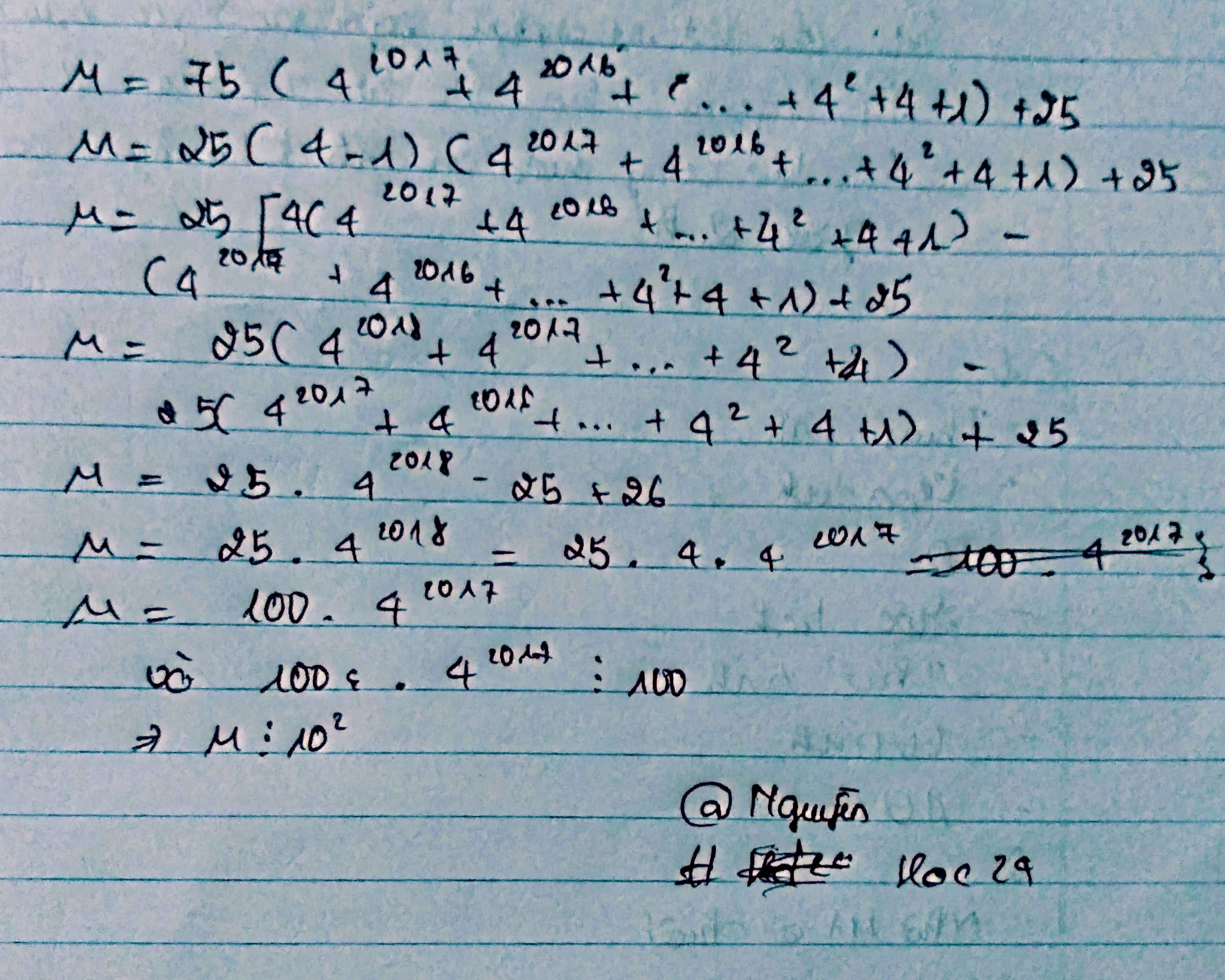
Đặt \(A_1=\left(1+4+4^2+...+4^{2016}+4^{2017}\right)\)
Ta có: \(A_1=\left(1+4+4^2+...+4^{2016}+4^{2017}\right)\)
\(\Leftrightarrow4A_1=4+4^2+4^3+...+4^{2017}+4^{2018}\)
Lấy \(4A_1-A_1\)ta có:
\(4A_1-A_1=\left(4+4^2+4^3+...+4^{2017}+4^{2018}\right)-\left(1+4+4^2+...+4^{2016}+4^{2017}\right)\)
\(\Leftrightarrow3A_1=4^{2018}-1\)
\(\Leftrightarrow A_1=\frac{4^{2018}-1}{3}\)
Thay \(A_1=\frac{4^{2018}-1}{3}\)vào biểu thức A, ta có:
\(A=75.\left(\frac{4^{2018}-1}{3}\right)+25\)
\(\Leftrightarrow A=25.\left(4^{2018}-1\right)+25\)
\(\Leftrightarrow A=25.4^{2018}⋮4^{2018}\)
Vậy \(A⋮4^{2018}\)
chúc bn hok tốt
thanks bro