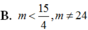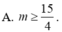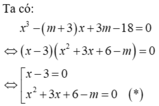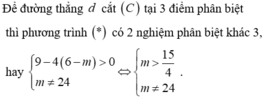cho y=x3-3x+1(C) và (d) y=mx+m+3. có bao nhiêu giá trị thực m để (d) cắt (C) tại 3 điểm phân biệt M(-1;3),N,P sao cho tiếp tuyến của (C) tại N,P vuông góc với nhau?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Đáp án A
Xét phương trình hoành độ giao điểm:
x 3 − 3 x 2 + 1 − m x + m + 1 = 0
⇔ x − 1 x 2 − 2 x − m − 1 = 0 ⇔ x = 1 g x = x 2 − 2 x − m − 1 = 0
Yêu cầu bài toán ⇔ g x = 0 có 2 nghiệm phân biệt
⇔ Δ g x > 0 g x ≠ 0 ⇔ m > − 2
=>Có 1 giá trị m thỏa mãn

Pt hoành độ giao điểm:
\(x^3-6x^2+9x=mx\)
\(\Leftrightarrow x\left(x^2-6x+9-m\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x^2-6x+9-m=0\left(1\right)\end{matrix}\right.\)
d cắt (P) tại 3 điểm pb khi và chỉ khi (1) có 2 nghiệm pb khác 0
\(\Leftrightarrow\left[{}\begin{matrix}m\ne9\\\Delta'=9-\left(9-m\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ne9\\m>0\end{matrix}\right.\)