\(f'\left(x\right)=2cos2x-4\left(1-2m\right)sin2x-2m\)

Phương trình \(f'\left(x\right)=0\) có nghiệm

\(\Leftrightarrow2cos2x-4\left(1-2m\right)sin2x=2m\) có nghiệm

\(\Leftrightarrow cos2x-2\left(1-2m\right)sin2x=m\)

Theo điều kiện có nghiệm của pt lượng giác bậc nhất:

\(1^2+4\left(1-2m\right)^2\ge m^2\)

\(\Leftrightarrow15m^2-16m+5\ge0\)

\(\Leftrightarrow15\left(m-\dfrac{8}{15}\right)^2+\dfrac{11}{15}\ge0\) (luôn đúng)

Vậy \(f'\left(x\right)=0\) có nghiệm với mọi m

\(sin2x=-\dfrac{1}{2}\Leftrightarrow\left[{}\begin{matrix}2x=-\dfrac{\pi}{6}+k2\pi\\2x=\dfrac{7\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{12}+k\pi\\x=\dfrac{7\pi}{12}+k\pi\end{matrix}\right.\)

\(\Rightarrow\left\{{}\begin{matrix}\alpha=-\dfrac{\pi}{12}\\\beta=\dfrac{7\pi}{12}\end{matrix}\right.\) \(\Rightarrow\alpha^2+\beta^2=\dfrac{25\pi^2}{72}\)

Đáp án B

Đáp án D

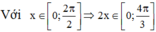
dựa vào đường tròn lượng giác suy ra PT có đúng hai nghiệm khi

Đáp án: B.

Các phương trình còn lại có nhiều hơn một nghiệm:

(x - 5)( x 2  - x - 12) = 0 có các nghiệm x = 5, 4, -3.

sin 2 x - 5sinx + 4 = 0 ⇔ sinx = 1, có vô số nghiệm

sinx - cosx + 1 = 0 có các nghiệm x = 0, x = 3 π /2

Đáp án: B.

Các phương trình còn lại có nhiều hơn một nghiệm:

(x - 5)( x 2  - x - 12) = 0 có các nghiệm x = 5, 4, -3.

sin 2 x  - 5sinx + 4 = 0 ⇔ sinx = 1, có vô số nghiệm

sinx - cosx + 1 = 0 có các nghiệm x = 0, x = 3π/2.