Gọi H là trực tâm tam giác ABC và O là giao 3 đường trung trực của tg ABC

=> O là tâm đường tròng ngoại tiếp tg ABC

Nối A với O kéo dài cắt (O) tại D

Xét tứ giác BHCD có

BH vuông góc AC

^ACD=90 (góc nt chắn nửa đường tròn)

=> CD vuông góc AC

=> BH//CD (BH, CD cùng vuông góc với AC) (1)

CH vuông góc AB

^ABD=90 (góc nt chắn nửa đường tròn)

=> BD vuông góc AB

=> CH//BD (CH, BD cùng vuông góc với AB) (2)

Từ (1) và (2) => BHCD là hình bình hành (Tứ giác có các cặp cạnh đối // với nhau thì là hbh)

Gọi M là trung điểm BC => OM là đường trung trực của tg ABC thuộc cạnh BC => OM vuông góc với BC

AH vuông góc BC

=> AH//OM (cùng vuông góc với BC)

Xét hình bình hành BHCD

Do M là trung điểm của BC => M cũng là trung điểm của HD (trong hình bình hành hai đường chéo cắt nhau tại trung điểm mỗi đường)

=> Áp dụng talet trong tam giác \(\Rightarrow\frac{DM}{DH}=\frac{OM}{AH}=\frac{1}{2}\Rightarrow AH=2.OM\)

O là tâm đường tròn ngoại tiếp tam giác ABC nên ta vẽ đường kính AOE

Tứ giác BHCE là hình bình hành

M là trung điểm của BC. Do đó M là trung điểm của HE.

Kết hợp với O là trung điểm của AE suy ra OM là đường trung bình của \(\Delta AHE\)

\(\Rightarrow OM=\frac{1}{2}AH\)hay 2OM = AH

Vậy khoảng cách từ trực tâm tới đỉnh bằng 2 lần khoảng cách từ giao điểm các đường trung trực tới cạnh đối diện đỉnh đó (đpcm)

SÔNG CÓ KHÚC NGƯỜI CÓ LÚC MÀ BẠN .

TRÁCH BẠN ẤY LÀM GÌ 

ối trời ơi đến cả zZz Phan Cả Phát zZz cũng phải đi hỏi bài ư?

Thế mà gọi là thần đồng

~~~~

Câu hỏi của marivan2016 - Toán lớp 9 - Học toán với OnlineMath

Tham khảo nha!

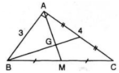
ΔABC vuông tại A có BC2 = AB2 + AC2 (định lí Pitago)

⇒ BC2 = 32 + 42 = 25 ⇒ BC = 5 (cm)

Gọi M là trung điểm của BC ⇒ AM là trung tuyến.

Vì theo đề bài: trong một tam giác vuông, đường trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên