TỨ GIÁC ABHK LÀ HCN DẤU HIỆU 1

B)

TAM GIÁC AHD= TAM GIÁC BCK (CH-CGV)VÌ

GÓC H = GÓC K ( CÙNG BẰNG 90 ĐỘ)

AH=AK(ABHK LÀ HCN)

AD=BC(ABCD LÀ HÌNH THANG CÂN)

SUY RA DH=KC ( HAI CẠNH TƯƠNG ỨNG)

a: Xét tứ giác ABCH có

AB//CH

góc AHC=90 độ

Do đó: ABCH là hình thang vuông

b: Sửa đề; DH=CK

Xét ΔAHD vuông tại H và ΔBKC vuông tại K có

AD=BC

góc D=góc C

Do đo: ΔAHD=ΔBKC

=>DH=CK

c: Xét ΔAED có

AH vừa là đường cao, vừa là trung tuyến

nên ΔAED cân tại A

=>góc AED=góc ADE=góc BCD

=>AE//BC

mà AB//CE

nên ABCE là hình bình hành

a: Xét tứ giác ABKH có 

AB//HK

AB=HK

Do đó: ABKH là hình bình hành

mà \(\widehat{AHK}=90^0\)

nên ABKH là hình chữ nhật

mình cần câu b

a: Xét tứ giác ABKH có 

AB//HK

AH//BK

Do đó: ABKH là hình bình hành

mà \(\widehat{AHK}=90^0\)

nên ABKH là hình chữ nhật

Xét hình thang cân ABCD ( AB // CD )

\(\Rightarrow\hept{\begin{cases}\widehat{D}=\widehat{C}\\AD=BC\end{cases}\left(t/c\right)}\)

Xét \(\Delta ADH=\Delta BCK\)

\(\hept{\begin{cases}\widehat{AHD}=\widehat{BKC}\left(=90^o\right)\\AD=BC\left(cmt\right)\\\widehat{D}=\widehat{C}\left(cmt\right)\end{cases}}\)

\(\Rightarrow\Delta ADH=\Delta BCK\)  ( ch - gn )

\(\Rightarrow AH=BK\) ( 2 cạnh tương ứng )
 b) Vì \(\Delta ADH=\Delta BCK\left(cmt\right)\)

\(\Rightarrow DK=CK\) ( 2 cạnh tương ứng )

Chúc bạn học tốt !!!

Áp dụng định nghĩa, tính chất và giả thiết của hình thang cân ta có:

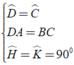
⇒ Δ ADH = Δ BCK

(trường hợp cạnh huyền – góc nhọn)

⇒ DH = CK (cặp cạnh tương ứng bằng nhau)

Vậy DH = CK. (đpcm)