Điều kiện xác định của biểu thức\(\dfrac{1}{\sqrt{x}-\sqrt{2x-1}}\)là
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Lời giải:
ĐKXĐ: \(\left\{\begin{matrix}
x^2-2x+1\neq 0\\
\frac{1}{x^2-2x+1}\geq 0\end{matrix}\right.\Leftrightarrow x^2-2x+1>0\)
$\Leftrightarrow (x-1)^2>0$
$\Leftrightarrow x-1\neq 0$
$\Leftrightarrow x\neq 1$

Sửa đề: \(A=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{3\sqrt{x}+1}{x-1}\)
a: ĐKXĐ: x>=0; x<>1
b: \(A=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{3\sqrt{x}+1}{x-1}\)
\(=\dfrac{\left(\sqrt{x}-1\right)^2+\left(\sqrt{x}+1\right)^2-3\sqrt{x}-1}{x-1}\)
\(=\dfrac{x+2\sqrt{x}+1+x-2\sqrt{x}+1-3\sqrt{x}-1}{x-1}\)
\(=\dfrac{2x-3\sqrt{x}+1}{x-1}=\dfrac{\left(\sqrt{x}-1\right)\cdot\left(2\sqrt{x}-1\right)}{x-1}\)
\(=\dfrac{2\sqrt{x}-1}{\sqrt{x}+1}\)
a) ĐKXĐ: \(x\ge0,x\ne1\)
b) \(A=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{3\sqrt{x}+1}{\sqrt{x}-1}\)
\(A=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{\sqrt{x}+1-3\sqrt{x}-1}{\sqrt{x}-1}\)
\(A=\dfrac{\sqrt{x}-1}{\sqrt{x}+1}+\dfrac{-2\sqrt{x}}{\sqrt{x}-1}\)
\(A=\dfrac{\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}-\dfrac{2\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(A=\dfrac{x-2\sqrt{x}+1-2x-2\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(A=\dfrac{-x-4\sqrt{x}+1}{x-1}\)

a/ ĐKXĐ : \(-2x+3\ge0\)
\(\Leftrightarrow x\le\dfrac{3}{2}\)
b/ ĐKXĐ : \(3x+4\ge0\)
\(\Leftrightarrow x\ge-\dfrac{4}{3}\)
c/ Căn thức \(\sqrt{1+x^2}\) luôn được xác định với mọi x
d/ ĐKXĐ : \(-\dfrac{3}{3x+5}\ge0\)
\(\Leftrightarrow3x+5< 0\)
\(\Leftrightarrow x< -\dfrac{5}{3}\)
e/ ĐKXĐ : \(\dfrac{2}{x}\ge0\Leftrightarrow x>0\)
P.s : không chắc lắm á!

ĐK:`4/(2x-1)>=0(x ne 1/2)`
Mà `4>0`
`<=>2x-1>0`
`<=>2x>1`
`<=>x>1/2`
Vậy `x>1/2` thì `sqrt{4/(2x-1)}` có nghĩa
\(DK:\left\{{}\begin{matrix}2x-1>0\\4\ge2x-1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{1}{2}\\x\le\dfrac{5}{2}\end{matrix}\right.\)
Vậy \(x\in(\dfrac{1}{2};\dfrac{5}{2}]\) hay \(\dfrac{1}{2}< x\le\dfrac{5}{2}\)

a) ĐKXĐ: \(x\ge0;x\ne1\)
b) \(P=\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{\sqrt{x}}{\sqrt{x}-1}\right):\dfrac{2}{\sqrt{x}+1}\left(x\ge0;x\ne1\right)\\ P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)-\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{2}\\ P=\dfrac{x-\sqrt{x}-x-\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{2}\\ P=\dfrac{-2\sqrt{x}}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\cdot\dfrac{\sqrt{x}+1}{2}\\ P=\dfrac{-\sqrt{x}}{\sqrt{x}-1}\)

a: ĐKXĐ: \(\dfrac{x-1}{5-x}\ge0\)
\(\Leftrightarrow\dfrac{x-1}{x-5}\le0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-1\ge0\\x-5< 0\end{matrix}\right.\Leftrightarrow1\le x< 5\)
b: ĐKXĐ: \(\left[{}\begin{matrix}x>3\\x< 2\end{matrix}\right.\)

1) ĐKXĐ: \(x\notin\left\{0;1\right\}\)
2) Ta có: \(A=\left(\dfrac{x\sqrt{x}-1}{x-\sqrt{x}}-\dfrac{x\sqrt{x}+1}{x+\sqrt{x}}\right):\left(1-\dfrac{3-\sqrt{x}}{\sqrt{x}+1}\right)\)
\(=\dfrac{x+\sqrt{x}+1-\left(x-\sqrt{x}+1\right)}{\sqrt{x}}:\dfrac{\sqrt{x}+1-3+\sqrt{x}}{\sqrt{x}+1}\)
\(=2\cdot\dfrac{\sqrt{x}+1}{2\sqrt{x}-2}\)
\(=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
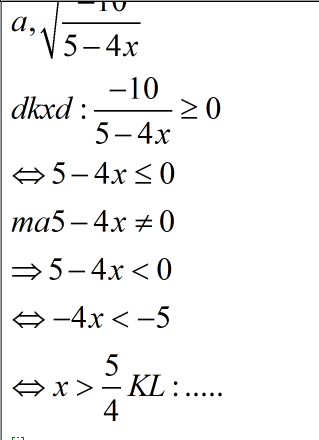
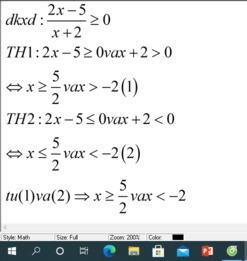
ĐKXĐ: \(\left\{{}\begin{matrix}x\ge\dfrac{1}{2}\\x\ne1\end{matrix}\right.\)