tìm tập xác định của hàm số y=f(x)=\(\sqrt{\frac{1+tanx}{1-tanx}}\)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cộng đồng học tập online | Học trực tuyến
Lần sau có bài em đăng trong link này để đc các bạn giúp đỡ nhé!
+)\(y=\frac{1}{\sqrt{1+\cos4x}}\)
ĐKXĐ: \(\cos4x+1>0\Leftrightarrow\cos4x>-1\Leftrightarrow\cos4x\ne-1\)
\(\Leftrightarrow4x\ne\pi+k2\pi\Leftrightarrow x\ne\frac{\pi}{4}+\frac{k\pi}{2}\), k thuộc Z
TXĐ: \(ℝ\backslash\left\{\frac{\pi}{4}+\frac{k\pi}{2}\right\}\), k thuộc Z
+) \(y=\sqrt{\tan x-\sqrt{3}}\)
ĐKXĐ: \(\hept{\begin{cases}\tan x-\sqrt{3}\ge0\\x\ne\frac{\pi}{2}+k\pi\end{cases}\Leftrightarrow\hept{\begin{cases}\tan x\ge\tan\frac{\pi}{3}\\x\ne\frac{\pi}{2}+k\pi\end{cases}\Leftrightarrow}\frac{\pi}{3}+k\pi\le x< \frac{\pi}{2}+k\pi}\)
TXĐ:...

1.
ĐKXĐ: \(\left\{{}\begin{matrix}cosx\ne0\\tanx-sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\\dfrac{sinx}{cosx}-sinx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}cosx\ne0\\sinx\ne0\\cosx\ne1\end{matrix}\right.\) \(\Leftrightarrow sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
2.
ĐKXĐ: \(sin2x\ne0\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
3.
ĐKXĐ: \(\left\{{}\begin{matrix}sin\left(x-\dfrac{\pi}{4}\right)\ne0\\cos\left(x-\dfrac{\pi}{4}\right)\ne0\end{matrix}\right.\)
\(\Leftrightarrow sin\left(2x-\dfrac{\pi}{2}\right)\ne0\Leftrightarrow cos2x\ne0\)
\(\Leftrightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)

Ban đầu bạn phân tích từ sin2x - 2 ≠ 0 thành sinx.cosx ≠ 1.
Sao đến cuối bạn lại biến sinx.cosx ≠ 1 thành sin2x ≠ \(\frac{1}{2}\)

ĐKXĐ: \(\left\{{}\begin{matrix}tanx\ne1\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{4}+k\pi\\x\ne\dfrac{\pi}{2}+k\pi\end{matrix}\right.\)

Ta có hàm số: \(y=\dfrac{1-cosx}{tanx}\) hàm số được xác định khi:
\(\left\{{}\begin{matrix}cosx\ne0\\tanx\ne0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+k\pi\\x\ne k\pi\end{matrix}\right.\left(k\in Z\right)\)
\(\Leftrightarrow x\ne\dfrac{k\pi}{2}\)
Tập xác định của y là:
\(D=R\backslash\left(\dfrac{k\pi}{2};k\in Z\right)\)

Điều kiện: cosx ≠ 0; sinx ≠ 0 và sin2x ≠ 1.
⇔ x ≠ kπ/2, k ∈ Z và x ≠ π/4 + kπ, k ∈ Z.
Vậy tập xác định của hàm số là
D \ R [(kπ/2,k ∈ Z)] ∪ [(π/4 + kπ,k ∈ Z)].

Điều kiện: cos(x- π/3) ≠ 0 và tan(x- π/3) ≠ -1.
⇔ x- π/3 ≠ π/2 + kπ, k ∈ Z và x- π/3 ≠ (-π)/4 + kπ, k ∈ Z.
⇔ x ≠ 5π/6 + kπ, k ∈ Z và x ≠ π/12 + kπ, k ∈ Z.
Vậy tập xác định của hàm số là
D = R \ [(5π/6 + kπ,k ∈ Z)] ∪ [(π/12 + kπ,k ∈ Z)].

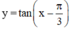 xác định
xác định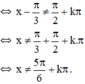
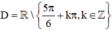

ĐKXĐ: \(\left\{{}\begin{matrix}\frac{1+tanx}{1-tanx}\ge0\\tanx\ne1\\cosx\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-1\le tanx< 1\\x\ne\frac{\pi}{2}+k\pi\end{matrix}\right.\)
\(\Rightarrow-\frac{\pi}{4}+k\pi\le x< \frac{\pi}{4}+k\pi\)