Đáp án: C

- Gọi  m 2  là khối lượng của chất lỏng chứa trong bình 2 (ở C), m là khối lượng của mỗi ca chất lỏng đổ vào (có nhiệt độ ).

- Phương trình cân bằng nhiệt ứng với lần đổ thứ 1 là:

Lần 1:

    m 2 . c ( 17 , 5 - 10 ) = m . c ( t 1 - 17 , 5 )

    ⇒ m 2 ( 17 , 5 - 10 ) - m ( t 1 - 17 , 5 )

    ⇒ 7 , 5 m 2 = m ( t 1 - 17 , 5 )   ( 1 )

- Từ lúc ban đầu đến lần đổ cuối học sinh đó đã đổ 3 ca chất lỏng. Coi như học sinh ấy đổ 1 lần 3 ca chất lỏng, thì nhiệt độ bình 2 tăng từ 10 0 C lên thành 25°C. Ta có phương trình:

    m 2 ( 25 - 10 ) = 3 m ( t 1 - 25 )

    ⇒ 15 m 2 = 3 m ( t 1 - 25 )   ( 2 )

- Từ (1) và (2)

⇒ 3.( t 1  – 25) = 2( t 1  – 17,5)

⇒ = 40 0 C

Đáp án: D

- Gọi m 2  là khối lượng của chất lỏng chứa trong bình 2 sau lần đổ thứ nhất (ở 20 0 C ), m là khối lượng của mỗi ca chất lỏng đổ vào (có nhiệt độ ) và t là nhiệt độ bỏ sót không ghi. Phương trình cân bằng nhiệt ứng với lần đổ thứ 2 là:

- Lần 2:

    m 2 . c ( 30 - 20 ) = m . c ( t 1 - 30 )

    ⇒ m 2 ( 30 - 20 ) = m ( t 1 - 30 )

    ⇒ 10 m 2 = m ( t 1 - 30 )   ( 1 )

- Từ lần đổ thứ nhất đến lần đổ cuối học sinh đó đã đổ 3 ca chất lỏng. Coi như học sinh ấy đổ 1 lần 3 ca chất lỏng, thì nhiệt độ bình 2 tăng từ  20 0 C  lên thành  40 0 C . Ta có phương trình:

    m 2 ( 40 - 30 ) = 3 m ( t 1 - 40 )

    ⇒ 20 m 2 = 3 m ( t 1 - 40 )   ( 2 )

- Từ (1) và (2)

   ⇒ 3.( t 1  – 40) = 2( t 1  – 30)

   ⇒  t 1  =60°C

- Thay vào (1) ta có:

    10 m 2 = m ( t 1 - 30 ) = 30 m ⇒ m 2 = 3 m

Lần 3:

    ( m 2 + m ) ( t - 30 ) = m ( 60 - t )

   ⇒ 4m.(t-30) = m(60 – t)

⇒ t = 36 0 C

* đổ lần 1

\(=>m\)(bình 1)\(=m2+m1\left(kg\right)\)

*đổ lần 2:

\(=>Qtoa1=m2.C.\left(t-35\right)\left(J\right)\)

\(=>Qthu1=\left(m1+m2\right)C.\left(35-20\right)\left(J\right)\)

\(=>m2.C.\left(t-35\right)=\left(m1+m2\right)C.15\left(J\right)\)(1)

*đổ lần 3:

\(=>Qthu2=\left(m1+m2\right)C.\left(t3-20\right)\left(J\right)\)

\(=>Qtoa2\)\(=2m2.C\left(t-t3\right)\left(J\right)\)

\(=>2m2C\left(t-t3\right)=\left(m1+m2\right)C\left(t3-20\right)\left(2\right)\)

lấy(2) chia(1)\(=>\dfrac{2\left(t-t3\right)}{t-35}=\dfrac{t3-20}{15}\left(3\right)\)

*đổ lần 4:

\(=>Qthu3=\left(m1+m2\right)C\left(50-20\right)\left(J\right)\)

\(=>Qtoa3=3m2.C\left(t-50\right)\)

\(=>3m2.C\left(t-50\right)=\left(m1+m2\right)C.30\left(4\right)\)

lấy (4) chia(1)

\(=>\dfrac{3\left(t-50\right)}{t-35}=\dfrac{30}{15}=>t=80^oC\left(5\right)\)

thế(5) vào (3)\(=>\dfrac{2\left(80-t3\right)}{80-35}=\dfrac{t3-20}{15}=>t3=44^oC\)

Gọi khối lượng, nhiệt dung riêng của bình 1 và từng ca chất lỏng của bình 2 lần lượt là m₁; c₁ và m₂; c₂.

Nhiệt dung tương ứng q₁ = m₁.c₁ và q₂ = m₂.c₂

Nhiệt độ ban đầu của bình 2 là t₂, nhiệt độ lần bỏ sót không ghi là t_x.

Phương trình cân bằng nhiệt sau lần trút thứ 2 là:

q₂.( t₂ – 35 ) = ( q₁ + q₂ ).( 35 – 20 ) => 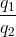= 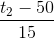(1)

Phương trình cân bằng nhiệt sau lần trút thứ 3 là:

q₂.( t₂ – t_x ) = ( q₁ + 2q₂ ).( t_x – 35 ) (2)

Phương trình cân bằng nhiệt cho lần trút cuối cùng là:

q₂.( t₂ – 50 ) = ( q₁ + 3q₂ ).( 50 - t_x ) (3)

Thay (1) vào (2) => t_x = 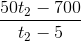(4)

Thay (1) vào (3) => t_x = 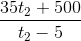(5)

Từ (4) và (5) => t₂ = 80^oC thay t₂ = 80^oC vào (5) => t_x = 44^oC

Vậy nhiệt độ lần bỏ sót là 44^oC

dung ko vay

* Gọi khối lượng mỗi ca chất lỏng múc từ bình 1 và khối lượng chất lỏng bình 2 bạn đầu lần lượt là m0m0 và mm
+ Sau khi đổ lần 1 có k/l chất lỏng bình 2 là (m+m0)(m+m0) và t1=100Ct1=100C
+ Sau khi đổ lần 2 ta có Pt cbn: c(m+m0)(t2−t1)=c.m0.(t0−t2)(∗)c(m+m0)(t2−t1)=c.m0.(t0−t2)(∗)
+ Sau khi đổ lần 3 ta có Pt cbn: c(m+m0)(t3−t1)=2cm0(t0−t3)(∗∗)c(m+m0)(t3−t1)=2cm0(t0−t3)(∗∗) ( Viết PT coi như đổ 2 ca sau lần đổ đầu tiên)
+ Sau khi đổ lần 4 ta có Pt cbn: c(m+m0).(t4−t1)=3cm0(t0−t4)(∗∗∗)c(m+m0).(t4−t1)=3cm0(t0−t4)(∗∗∗) ( Viết PT coi như đổ 3 ca sau lần đổ đầu tiên)
- Từ (*) vs (***)\(\Rightarrow\dfrac{t_2-t_1}{t_4-t_1}=\dfrac{t_0-t_2}{3.\left(t_0-t_4\right)}=...\Rightarrow t_0=...\)

- Từ (*) & (**):\(\Rightarrow\dfrac{t_2-t_1}{t_3-t_1}=\dfrac{t_0-t_2}{2\left(t_0-t_3\right)}=...\Rightarrow t_3=...\)

thánh này đăng nhìu bài v

Giả sử khối lượng của chất lỏng mỗi bình là \(\dfrac{m}{2}\)

a) Sau vài lần rót thì khối lượng chất lỏng trong các bình lần lượt là: 

Bình 3: \(m\)

Bình 2: \(\dfrac{m}{3}\)

Bình 1: \(\dfrac{m}{6}\)

\(Q_{tỏa}=m.c.(80-50)=m.c.30\)

\(Q_{thu}=\dfrac{m}{6}.c.\Delta t+\dfrac{m}{3}.c.(48-40)=\dfrac{m}{6}.c.\Delta t+\dfrac{m}{3}.c.8\)

\(Q_{tỏa}=Q_{thu}\Rightarrow 30=\dfrac{\Delta t}{6}+\dfrac{8}{3}\Rightarrow \Delta t\Rightarrow t\)

(Kết quả có vẻ hơi vô lý, bạn xem lại giả thiết nhé)

b) Sau khi rót đi rót lại nhiều lần, nhiệt độ của chất lỏng trong các bình bằng nhau và bằng t

\(\Rightarrow \dfrac{m}{2}.c(t-20)+\dfrac{m}{2}.c.(t-40)=\dfrac{m}{2}.c.(80-t)\)

\(\Rightarrow (t-20)+(t-40)=(80-t)\Rightarrow t = 46,67^0C\)

bạn ơi cái phần b đó.sao lượng nước ở 3 bình lại bằng nhau?