Ai giúp với ạ mình đang cần gấp
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



\(P=\left[\dfrac{x\left(x-2\right)}{2\left(x^2+4\right)}-\dfrac{2x^2}{\left(2-x\right)\left(x^2+4\right)}\right]\cdot\dfrac{x^2-x-2}{x^2}\\ P=\dfrac{-x\left(x-2\right)^2-4x^2}{2\left(x^2+4\right)\left(2-x\right)}\cdot\dfrac{\left(x-2\right)\left(x+1\right)}{x^2}\\ P=\dfrac{x^3+4x}{2\left(x^2+4\right)\left(x-2\right)}\cdot\dfrac{\left(x-2\right)\left(x+1\right)}{x^2}\\ P=\dfrac{x\left(x^2+4\right)\left(x+1\right)}{2x^2\left(x^2+4\right)}=\dfrac{x+1}{2x}\)

Bài1:Tại vì châm lửa lửa sẽ tác dụng với oxi để cháy
Bài2:vì nó sẽ đẩy nhiều oxi vào bên trong oxi sẽ tác dụng vs lửa và cháy to hơn bạn đầu
Bài3: thổi mạnh vào ngọn nến thì ngọn nến sẽ tắt vì khí mình thổi ra là khí cacbonic
Chúc bạn học tốt

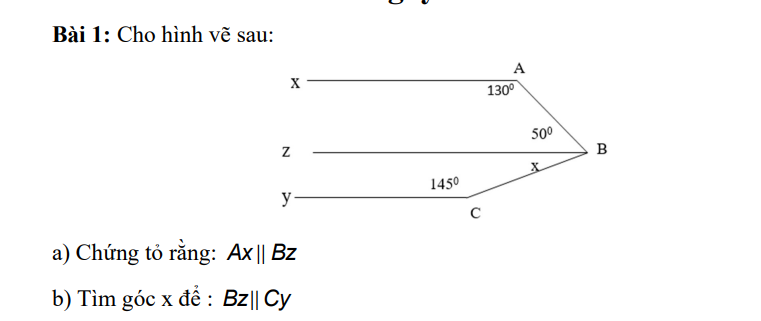
\(\widehat{XAB}\) + \(\widehat{ABZ}\) = 1300 + 500 = 1800
Vì góc XAB và góc ABZ là hai góc trong cùng phía nên
Ax // BZ
BZ // Cy ⇔ \(x\) + \(\widehat{yCB}\) =1800
⇒ \(x\) = 1800 - 1450 = 350


Bài 1:
a, \(\)\(\)\(=>R2//\left[R4nt\left(R3//R5\right)\right]\)
\(=>Rtd=\dfrac{R2\left[R4+\dfrac{R3.R5}{R3+R5}\right]}{R2+R4+\dfrac{R3.R5}{R3+R5}}=\dfrac{1.\left[1+\dfrac{1}{1+1}\right]}{1+1+\dfrac{1}{1+1}}=0,6\left(ôm\right)\)
\(=>I=\dfrac{Uab}{Rtd}=\dfrac{10}{0,6}=\dfrac{50}{3}A=I1\)
\(=>Uab=U2345=10V=U2=U345\)
\(=>I2=\dfrac{U2}{R2}=\dfrac{10}{1}=10A\)
\(=>I345=\dfrac{U345}{R345}=\dfrac{10}{1+\dfrac{1.1}{1+1}}=\dfrac{20}{3}A=I4=I35\)
\(=>U35=I35.R35=\dfrac{20}{3}.\dfrac{1.1}{1+1}=\dfrac{10}{3}V=U3=U5\)
\(=>I3=\dfrac{U3}{R3}=\dfrac{\dfrac{10}{3}}{1}=\dfrac{10}{3}A,\)
\(=>I5=\dfrac{U5}{R5}=\dfrac{10}{3}A\)
b, \(I1=0,1A=Im=I2345\)
\(=>Uab=I2345.R2345=0,1.\dfrac{6\left[8+\dfrac{6.12}{6+12}\right]}{6+8+\dfrac{6.12}{6+12}}=0,4V\)

\(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^2.10^2}\)
=\(\dfrac{3}{1.4}+\dfrac{5}{4.9}+...+\dfrac{19}{81.100}\)
=\(1-\dfrac{1}{4}+\dfrac{1}{4}-\dfrac{1}{9}+...+\dfrac{1}{81}-\dfrac{1}{100}\)
=\(1-\dfrac{1}{100}=\dfrac{99}{100}\)
Mà \(\dfrac{99}{100}< 1\) nên \(\dfrac{3}{1^2.2^2}+\dfrac{5}{2^2.3^2}+...+\dfrac{19}{9^2.10^2}< 1\)
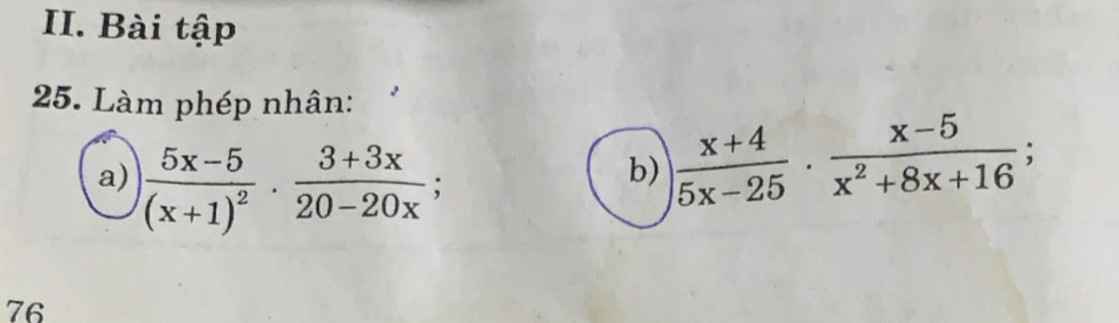
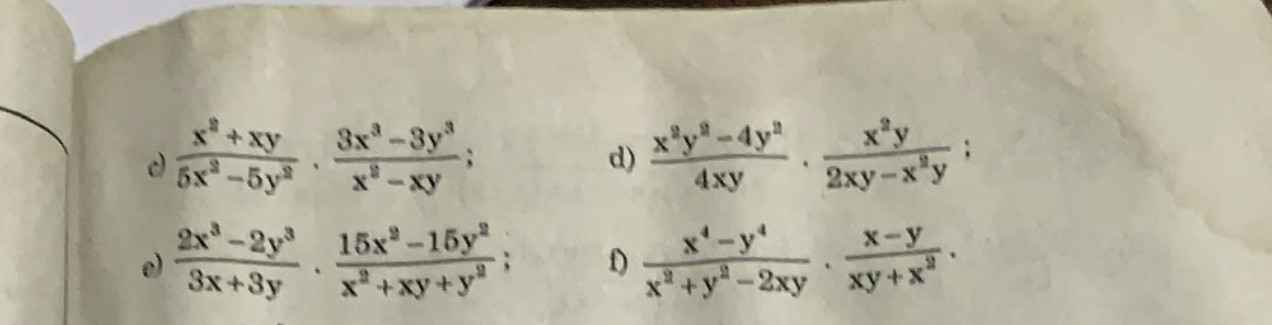



 ai làm giúp mình với mình đang cần gấp lắm ạ
ai làm giúp mình với mình đang cần gấp lắm ạ
 ai giúp mình bài 3 với ạ, mình đang cần gấp, mình cảm ơn
ai giúp mình bài 3 với ạ, mình đang cần gấp, mình cảm ơn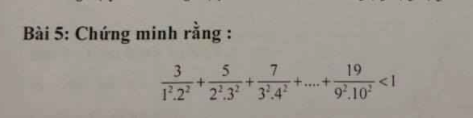 đang cần gấp bài 5 ai giúp mình với ạ :))
đang cần gấp bài 5 ai giúp mình với ạ :))