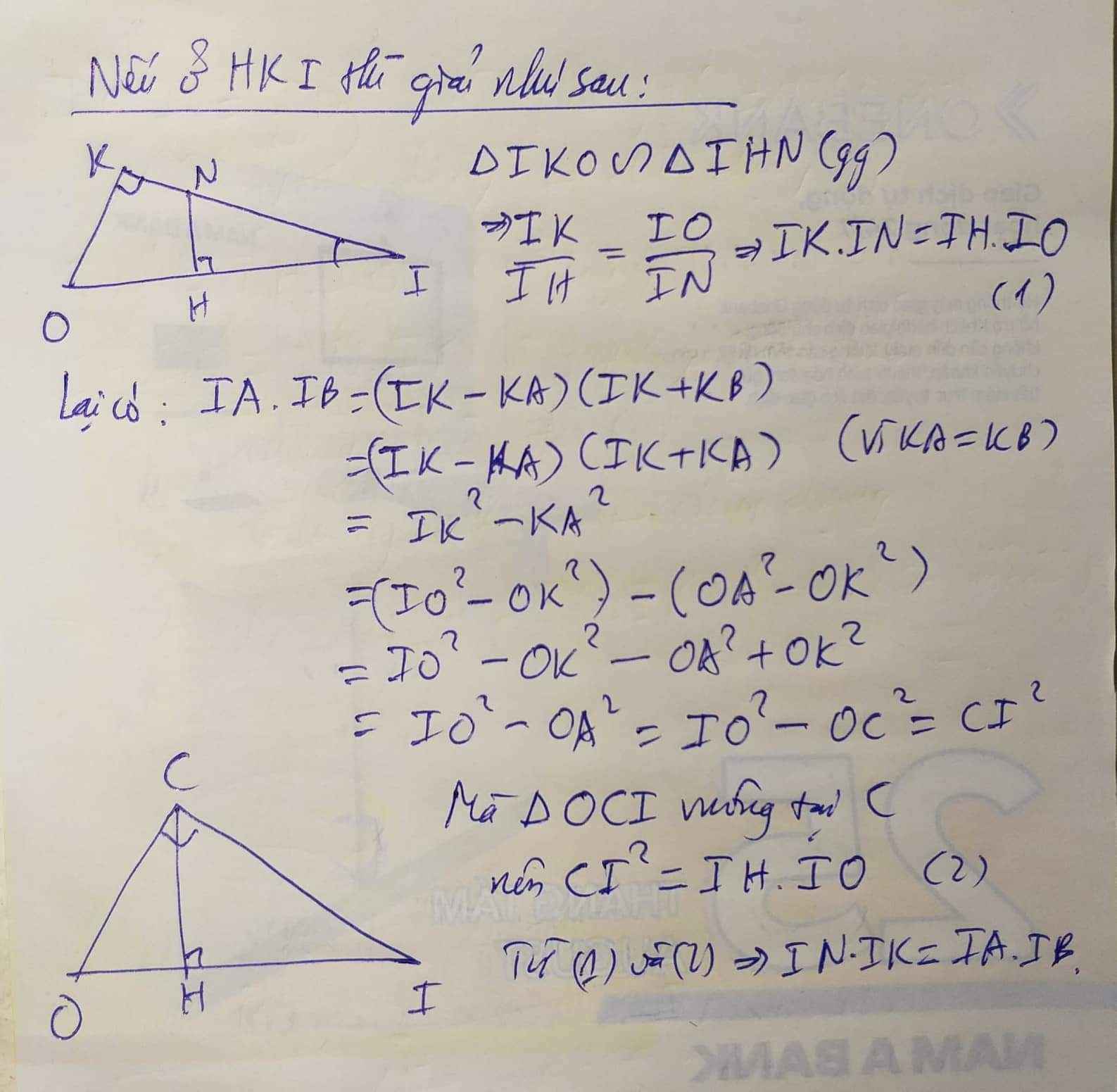Từ điểm I ở ngoài đường tròn tâm O, kẻ một đường thẳng không qua tâm O và cắt (O) tại A, b( IA< IB). Các tiếp tuyến với (O) tại A và :B cắt nhau ở M Kẻ MH vuông góc với OI tại H,MH cắt đường tròn (O) tại C, D (MC < MD); AB cắt MH, OM lần lượt tại N, K.
a) CMR K là t/đ AB và bốn điểm M,O,B,H cùng thuộc một đường tròn.
b) CMR OH.OI=OK.OM
c) CMR ID là tiếp tuyến của (O)
d) Gọi P,Q lần lượt là tâm đương tròn ngoại tiếp các tam giác NHK, CDK. Chứng minh rằng IN.IK=IA.IB và PQ vuông góc với OM
câu a b c dễ nên cần giúp d thôi. ý tưởng của mình về ý đầu tiên là cm IAQ đồng dạng IOB và ý thứ hai là CM O là giao điểm của (Q) và (P) ngoài C ra.