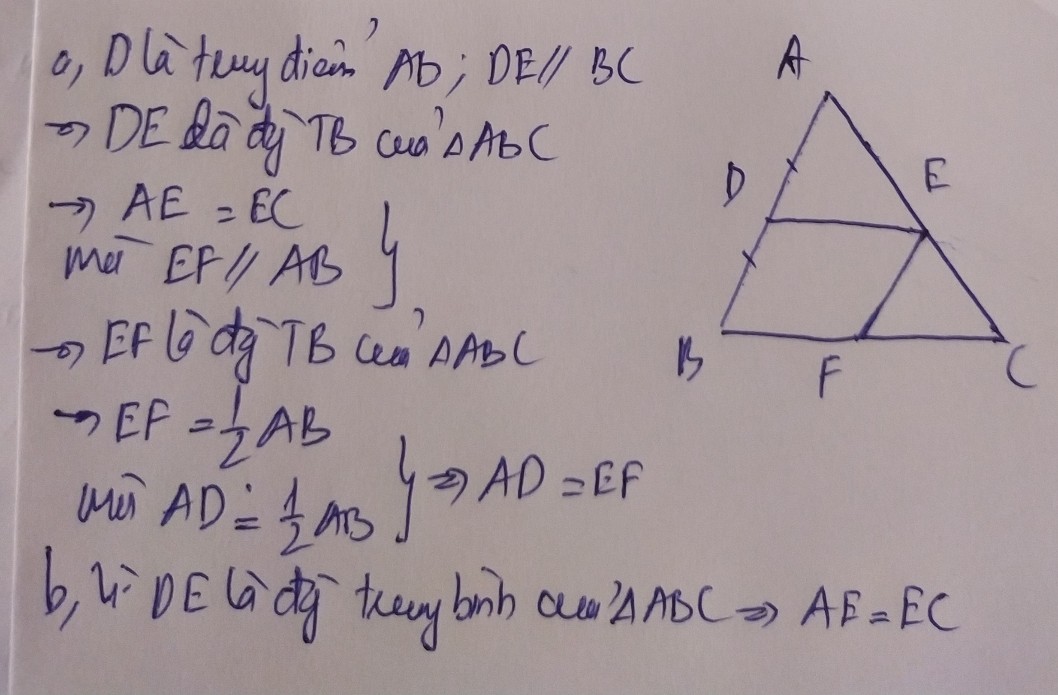Cho tam giác ABC có E là trung điểm của AC. Qua E kẻ ED//AB (D thuộc BC); EF//BC (F thuộc AB)
a)CMR: tứ giác BDEF là hình bình hành và D là trung điểm của đoạn thẳng BC
b)Gọi H là điểm đối xứng của D qua F . Chứng minh HB//AD
c)Gọi I là trung điểm của HB : K là giao điểm của AD và EF . CMR I,K,E thẳng hàng
d) Tam giác ABC cần thêm điều kiện Gì để HF=\(\frac{AB}{2}\)
Mọi ng ơi giúp mik vs mik cần gấp cảm ơn mọi ng nhiều !!!
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔABC có
E là trung điểm của AC
ED//AB
Do đó: D là trung điểm của BC
Xét ΔABC có
E là trung điểm của AC
EF//BC
Do đó: F là trung điểm của AB
Xét ΔABC có
F là trung điểm của AB
E là trung điểm của AC
Do đó: FE là đường trung bình của ΔBAC
Suy ra: FE//BD và FE=BD
hay FEDB là hình bình hành

a: Xét tứ giác AFCD có
E là trung điểm chung của AC và FD
=>AFCD là hình bình hành
b: EG//AB
AB\(\perp\)AC
Do đó: EG\(\perp\)AC
c:
Ta có: ΔABC vuông tại A
=>\(S_{ABC}=\dfrac{1}{2}\cdot AB\cdot AC=\dfrac{1}{2}\cdot3\cdot4=6\left(cm^2\right)\)

Vì D là trung điểm BC mà DE//AC nên E là trung điểm AB
Do đó DE là đường trung bình tam giác ABC
Vậy \(DE=\dfrac{1}{2}AC\) hay \(AC=2DE\)

a: Xét ΔABC có \(BC^2=AB^2+AC^2\)
nên ΔABC vuông tại A
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
BA=BE
Do đó:ΔABD=ΔEBD
Suy ra: góc ABD= góc EBD
hay BD là tia phân giác của góc ABC
c: Xét ΔADF vuông tại A và ΔEDC vuông tại E có
DA=DE
\(\widehat{ADF}=\widehat{EDC}\)
Do đó: ΔADF=ΔEDC
Suy ra: DF=DC
mà DC>DE
nên DF>DE
d: Đề sai rồi bạn

a)Xét tứ giác AFDE có :góc AED = 90°(gt)góc EAF = 90 °(gt)góc AFD =90 °(gt)=> Tứ giác AFDE là hình chữ nhật ( dhnb)(đcpcm)
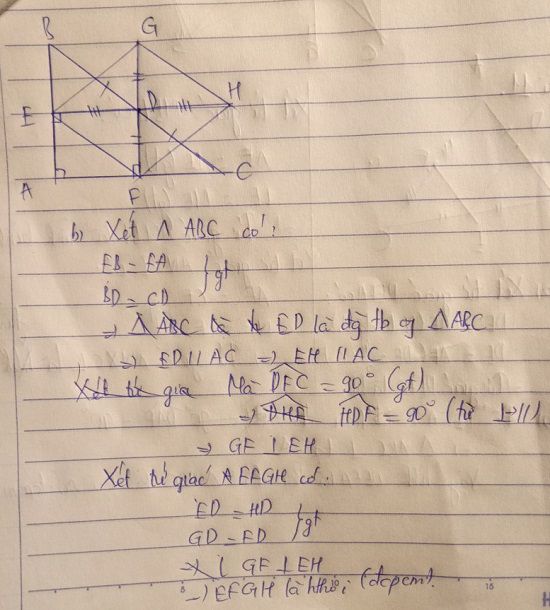


1: Xét ΔABC có
D là trung điểm của BC
DE//AC
Do đó: E là trung điểm của AB