Phương trình có nghiệm x = 1 => Khi phân tích thành nhân tử có nhân tử (x-1)
Vậy phương trình có nghiệm \(x=3+2\sqrt{2}\) thì có nhân tử là gì
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

3x2 + 8x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ’ = 42 – 2.3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:


* Chứng minh:
Phương trình a x 2 + b x + c = 0 có hai nghiệm x 1 ; x 2
⇒ Theo định lý Vi-et: 
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 
= a . x 2 + b x + c ( đ p c m ) .
* Áp dụng:
a) 2 x 2 – 5 x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 
Vậy: 
b) 3 x 2 + 8 x + 2 = 0
Có a = 3; b' = 4; c = 2
⇒ Δ ’ = 4 2 – 2 . 3 = 10 > 0
⇒ Phương trình có hai nghiệm phân biệt:


* Chứng minh:
Phương trình ax2 + bx + c = 0 có hai nghiệm x1; x2
⇒ Theo định lý Vi-et: 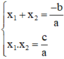
Khi đó : a.(x – x1).(x – x2)
= a.(x2 – x1.x – x2.x + x1.x2)
= a.x2 – a.x.(x1 + x2) + a.x1.x2
= 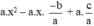
= a.x2 + bx + c (đpcm).
* Áp dụng:
a) 2x2 – 5x + 3 = 0
Có a = 2; b = -5; c = 3
⇒ a + b + c = 2 – 5 + 3 = 0
⇒ Phương trình có hai nghiệm 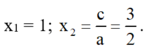
Vậy: 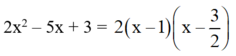

(IMO 2016 mà đưa vô đây chi?)
Dễ thấy nếu xoá ít hơn 2016 nhân tử thì không được, vì khi đó ở hai vế sẽ có nhân tử chung.
Ta sẽ CM có thể xoá đúng 2016 nhân tử, bằng cách:
\(\left(x-1\right)\left(x-4\right)\left(x-5\right)\left(x-8\right)...=\left(x-2\right)\left(x-3\right)\left(x-6\right)\left(x-7\right)...\)
Tự CM pt này vô nghiệm nha bạn.

a) Phương trình 2x2 – 5x + 3 = 0 có a + b + c = 2 – 5 + 3 = 0 nên có hai nghiệm là x1 = 1, x2 = \(\dfrac{3}{2}\) nên:
2x2 – 5x + 3 = 2(x – 1)(x2 - \(\dfrac{3}{2}\)) = (x – 1)(2x – 3)
b) Phương trình 3x2 + 8x + 2 có a = 3, b = 8, b’ = 4, c = 2.
Nên ∆’ = 42 – 3 . 2 = 10, có hai nghiệm là:
x1 = \(\dfrac{-4-\sqrt{10}}{3}\), x2 = \(\dfrac{-4+\sqrt{10}}{3}\)
nên: 3x2 + 8x + 2 = 3(x - \(\dfrac{-4-\sqrt{10}}{3}\))(x - \(\dfrac{-4+\sqrt{10}}{3}\))
= 3(x + \(\dfrac{4+\sqrt{10}}{3}\))(x + \(\dfrac{4-\sqrt{10}}{3}\))

Lời giải:
a. $x^3-4x^2+x+6=(x^3-2x^2)-(2x^2-4x)-(3x-6)$
$=x^2(x-2)-2x(x-2)-3(x-2)=(x-2)(x^2-2x-3)$
$=(x-2)[(x^2+x)-(3x+3)]=(x-2)[x(x+1)-3(x+1)]$
$=(x-2)(x+1)(x-3)$
-------------------
b.
$x^3+7x^2+14x+8=(x^3+x^2)+(6x^2+6x)+(8x+8)$
$=x^2(x+1)+6x(x+1)+8(x+1)=(x+1)(x^2+6x+8)$
$=(x+1)[(x^2+2x)+(4x+8)]=(x+1)[x(x+2)+4(x+2)]$
$=(x+1)(x+2)(x+4)$

Câu a bạn xem lại đề bài nhé. Đa thức đề cho thậm chí còn không có nghiệm hữu tỉ luôn cơ.
b) Lập sơ đồ Horner:
| 1 | 7 | 14 | 8 | |
| \(x=-1\) | 1 | 6 | 8 | 0 |
\(\Rightarrow x^3+7x^2+14x+8=\left(x+1\right)\left(x^2+6x+8\right)\)
Ta thấy đa thức \(g\left(x\right)=x^2+6x+8\), dự đoán được 1 nghiệm \(x=-2\). Ta lại lập sơ đồ Horner:
| 1 | 6 | 8 | |
| \(x=-2\) | 1 | 4 | 0 |
\(\Rightarrow g\left(x\right)=\left(x+2\right)\left(x+4\right)\)
Vậy đa thức đã cho có thể được phân tích thành \(\left(x+1\right)\left(x+2\right)\left(x+4\right)\)

a) Viết lại phương trình như sau: x2 - 3x + 2 - y - y2 = 0
Coi x là ẩn; y là tham số
ta có: \(\Delta\) = (-3)2 - 4(2 - y - y2 ) = 4y2 + 4y + 1 = (2y + 1)2 \(\ge\) 0 với mọi y
=> phương trình đã cho luôn có nghiệm là : \(x_1=\frac{3+2y+1}{2}=y+2;x_2=\frac{3-2y-1}{2}=1-y\)
b) x = y + 2 và x = 1 - y thoả mãn phương trình
=> y = x - 2 và y = 1 - x thoả mãn phương trình
c) do x = y + 2 và x = 1 - y là nghiệm của phương trình x2 - 3x + 2 - y - y2 = 0
=> x2 - 3x + 2 - y - y2 = (x - y - 2). (x - 1+ y)
*) Chú ý: Nếu x1; x2 là nghiệm của ax2 + bx + c = 0 => ax2 + bx + c = a.(x - x1)(x - x2)
Help!!
(x2+x+1)(x2+x+2)=12
x(x+1)(x2+x+1)=42
(x2+x+1)2= 3(x4+x2+1)
\(x=3+2\sqrt{2}\)
\(x-3-2\sqrt{2}=0\)
\(x-\left(3+2\sqrt{2}\right)=0\) Vậy nhân tử của \(x=3+2\sqrt{2}\) là \(x-\left(3+2\sqrt{2}\right)\)