Ở mặt thoáng của một chất lỏng có hai nguồn sóng kết hợp A và B cách nhau 20 cm, dao động theo phương thẳng đứng với phương trình u A = 2cos40πt và u B = 2cos(40πt + π) ( u A và u B tính bằng mm, t tính bằng s). Biết tốc độ truyền sóng trên mặt chất lỏng là 30 cm/s. Xét hình vuông AMNB thuộc mặt thoáng chất lỏng. Số điểm dao động với biên độ cực đại trên đoạn BM là
A. 18.
B. 20.
C. 19.
D. 17.

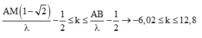

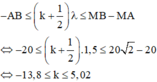

Đáp án C
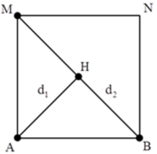
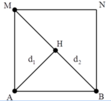
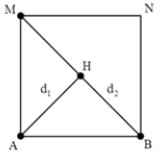
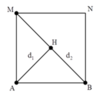
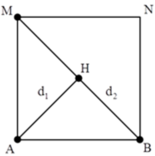
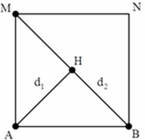
+ Gọi H là một điểm bất kì nằm trên BM. Tương tự, để H cực đại thì: d 1 - d 2 = k + 1 2 λ
+ Từ hình vẽ ta thấy khoảng giá trị của hiệu số d 1 - d 2 : A M - 2 A M ≤ d 1 - d 2 ≤ A B
+ Kết hợp hai phương trình trên ta thu được
A M 1 - 2 λ - 1 2 ≤ k ≤ A B λ - 1 2
→ - 6 , 02 ≤ k ≤ 12 , 8
Vậy sẽ có 19 điểm dao động với biên độ cực đại trên đoạn BM.