Cho hình bình hành ABCD với B A D ^ < 90 ∘ .
Đường phân giác của góc B C D ^ cắt đường tròn ngoại tiếp tam giác BCD tại O khác C.
Kẻ đường thẳng d đi qua A và vuông góc với CO.
Đường thẳng d lần lượt cắt các đường thẳng CB, CD tại E, F.
2). Chứng minh rằng O là tâm đường tròn ngoại tiếp tam giác △ C E F .
3). Gọi giao điểm của OC và BD là I, chứng minh rằng I B . B E . E I = I D . D F . F I .

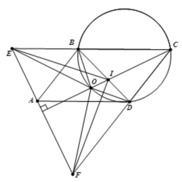
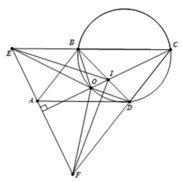

3). Theo trên, ta có B E = C D mà C E = C F ⇒ B C = D F .
Ta có CI là đường phân giác góc BCD, nên I B I D = C B C D = D F B E ⇒ I B . B E = I D . D F .
Mà CO là trung trực EF và I ∈ C O , suy ra IE=IF.
Từ hai đẳng thức trên, suy ra I B . B E . E I = I D . D F . F I .