Cho hàm số y = x 4 - 2 m 2 + 1 x 2 + 1 . Tìm giá trị của tham số m để hàm số này có 3 điểm cực trị thỏa mãn giá trị cực tiểu đạt giá trị lớn nhất.
A. m = 0
B. m = -1
C. m = -2
D. m = 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có
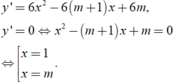
Để hàm số có hai điểm cực trị khi m khác -1
Tọa độ các điểm cực trị là A( 1; m3+ 3m-1) và B( m; 3m2)
Suy ra
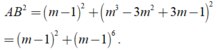
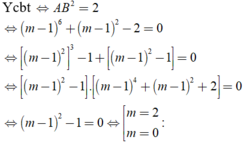
Chọn B.

Chọn B
y ' = m x 2 - 2 ( m - 1 ) x + 3 ( m - 2 )
Yêu cầu của bài toán
⇔
y
'
=
0
có hai nghiệm phân biệt
x
1
,
x
2
thỏa mãn:
x
1
+
2
x
2
=
1

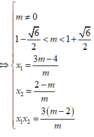

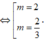

Đáp án D
Ta có y = m 3 x 3 + 2 x 2 + m x + 1 ⇒ y ' = m x 2 + 4 x + m ; ∀ x ∈ ℝ
Phương trình y ' = 0 ⇔ m x 2 + 4 x + m = 0 , có Δ = 4 − m 2
Yêu cầu bài toán tương đương với a = m 3 > 0 Δ ' > 0 ⇔ m > 0 4 − m 2 > 0 ⇔ 0 < m < 2
y ' = 4 x 3 - 4 m 2 + 1 x y ' = 0 ⇔ x = 0 x = ± m 2 + 1
Dễ thấy hàm số đã cho có 3 điểm cực trị với mọi m.
Với x C T = ± m 2 + 1 ⇒ giá trị cực tiểu y C T = - m 2 + 1 + 1
Ta có m 2 + 1 2 ≥ 1 ⇒ y C T ≤ 0 m a x y C T = 0 ⇔ m 2 + 1 = 1 ⇔ m = 0
Đáp án A