a. Gọi chữ số cần lập là \(\overline{abcd}\)

TH1: \(d=0\Rightarrow\) bộ abc có \(A_9^3\) cách chọn

TH2: \(d\ne0\Rightarrow d\) có 4 cách chọn (từ 2,4,6,8)

a có 8 cách chọn (khác 0 và d), b có 8 cách chọn (khác a và d), c có 7 cách chọn (khác a,b,d)

\(\Rightarrow4.8.8.7\) số

Tổng cộng: \(A_9^3+4.8.8.7=...\)

b. Chọn 4 chữ số còn lại: có \(C_7^4\) cách

Hoán vị 3 chữ số 0,1,2: có \(3!\) cách

Coi bộ 3 chữ số này là 1 số, hoán vị với 4 chữ số còn lại: \(5!\) cách

Ta đi tính số trường hợp 0 đứng đầu:

Số 0 đứng đầu trong bộ 0,1,2: có \(2!\) cách

Đặt bộ 0,1,2 đứng đầu, xếp vị trí cho 4 chữ số còn lại: \(4!\) cách

Vậy có: \(C_7^4.\left(3!.5!-2!.4!\right)=...\) số

a)     Số có ba chữ số khác nhau có thể lập được là: 6.5.4 = 120 (số)

b)    Số chia hết cho 3 nên tổng 3 chữ số chia hết cho 3, có các cặp số là: (1,2,3), (1,2,6), (2,3,4), (3,4,5), (4,5,6), (1,5,6), (1,3,5), (2,4,6).

Số có ba chữ số khác nhau và chia hết cho 3 có thể lập được là:

       8. 3! = 48 (số)

Cho \(X=\left\{0;1;2;4;5;6;8;9\right\}\)

Gọi số cần tìm là \(\overline{abcd}\)

Chọn \(d=1,d=5\) hay \(d=9\)\(\Rightarrow\) có 1 cách

Chọn \(a\) có \(6\) cách \(\left(a\ne0,a\ne d\right)\)

Chọn \(b\) có \(5\) cách \(\left(b\ne a,b\ne d\right)\)

Chọn \(c\) có \(4\) cách \(\left(c\ne a,c\ne b,c\ne d\right)\)

Theo Quy tắc nhân, ta có : \(1.6.5.4=120\) cách chọn 4 chữ số khác nhau và là số lẻ.

Đáp án B

Số đó nhất thiết phải có mặt 3 chữ số 1, 2, 5 ta chỉ cần chọn 2 chữ số nữa từ 4 chữ số còn lại.

TH1: Hai chữ số được chọn kia không chứa số 0: Ta có  

TH2: Hai chữ số kia chứa chữ số 0, ta loại trường hợp chữ số 0 đứng đầu thì còn: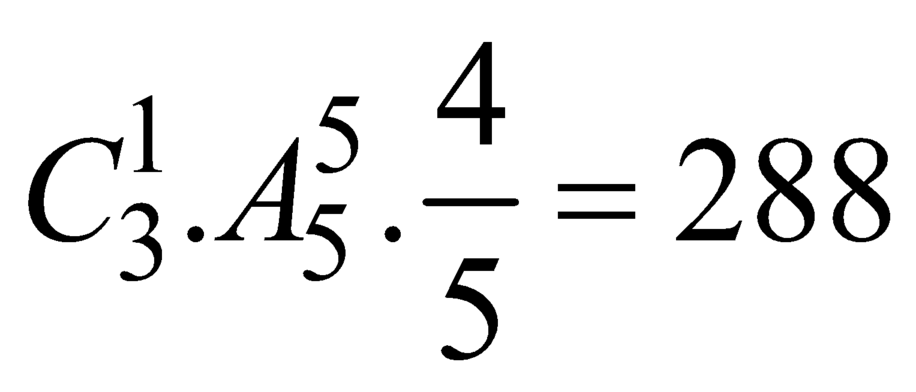  

Vậy có tất cả là 648 số

Gọi số cần lập 

Bước 1: Xếp chữ số 0 vào 1 trong 5 vị trí từ a₂ đến a₆, có 5 cách xếp.

Bước 2: Xếp chữ số 1 vào 1 trong 5 vị trí còn lại (bỏ 1 vị trí chữ số 0 đã chọn), có 5 cách xếp.

Bước 3: Chọn 4 chữ số trong 8 chữ số {2, 3, 4, 5, 6 , 7, 8, 9}để xếp vào 4 vị trí còn lại, có  cách.

Theo quy tắc nhân có   số thỏa yêu cầu.

Chọn D.

Từ 4 chữ số : 0; 1; 5; 2 có thể lập đc bao nhiêu số khác nhau có 3 chữ số mà chia hết cho cả 5 và 3

A, 7     B, 6     C, 5     D, 4

Đáp án đúng là D

HT~

TH1: số 2 đứng đầu:

Chọn 2 chữ số từ 6 chữ số còn lại và hoán vị: \(A_6^2=30\) cách

TH2: số 2 không đứng đầu:

Chọn số hàng trăm: có 5 cách (khác 0 và 2)

Chọn 1 chữ số còn lại: 5 cách, hoán vị nó với 2: có \(2!=2\) cách 

\(\Rightarrow5.5.2=50\) cách

Tổng cộng: \(30+50=80\) số