Trong các cặp số(x,y) thỏa mãn: \(\frac{x^2-x+y^2-y}{x^2+y^2-1}\le0\)Hãy tìm cặp số có tổng x+2y lớn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
16 tháng 11 2017
TH 1: \(x^2+y^2< 1\)
\(\Rightarrow\hept{\begin{cases}|x|< 1\\|y|< 1\end{cases}}\)
\(\Rightarrow S=x+2y\le\sqrt{2\left(x^2+y^2\right)}+y< 1+\sqrt{2}\left(1\right)\)
TH 2: \(x^2+y^2>1\)
\(\Rightarrow x^2-x+y^2-y\le0\)
\(\Leftrightarrow\left(S-2y\right)^2-\left(S-2y\right)+y^2-y\le0\)
\(\Leftrightarrow5y^2+\left(1-4S\right)y+S^2-S\le0\)
\(\Rightarrow\Delta=\left(1-4S\right)^2-4.5.\left(S^2-S\right)\ge0\)
\(\Leftrightarrow S\le\frac{5+\sqrt{10}}{2}\left(2\right)\)
Từ (1) và (2) suy ra được GTLN của S
PS: S là đặt cho nó gọn nhé
6 tháng 12 2020
Mình sửa đề như thế này không biết có đúng không:
"Trong các cặp số thực (x;y) thỏa mãn: \(\frac{x^2-x+y^2-y}{x^2+y^2-1}\le0\).
Hãy tìm cặp số có tổng x+2y lớn nhất."
Xét \(x^2+y^2>1\): (*) Khi đó phải có: \(x^2-x+y^2-y\le0\Leftrightarrow x^2+y^2\le x+y\). Áp dụng bất đẳng thức AM - GM ta có: \(x^2+\frac{7+2\sqrt{10}}{20}=x^2+\left(\frac{5+\sqrt{10}}{10}\right)^2\ge x.\frac{5+\sqrt{10}}{5}\); \(y^2+\frac{13+4\sqrt{10}}{20}=y^2+\left(\frac{5+2\sqrt{10}}{10}\right)^2\ge y.\frac{5+2\sqrt{10}}{5}\). Do đó: \(x^2+y^2+\frac{10+3\sqrt{10}}{10}\ge x.\frac{5+\sqrt{10}}{5}+y.\frac{5+2\sqrt{10}}{5}\) \(\Rightarrow x+y+\frac{10+3\sqrt{10}}{10}\ge x.\frac{5+\sqrt{10}}{5}+y.\frac{5+2\sqrt{10}}{5}\Leftrightarrow\frac{\sqrt{10}}{5}x+\frac{2\sqrt{10}}{5}y\le\frac{10+3\sqrt{10}}{10}\Leftrightarrow x+2y\le\frac{3+\sqrt{10}}{2}\). Đẳng thức xảy ra khi và chỉ khi \(x=\frac{5+\sqrt{10}}{5};y=\frac{5+2\sqrt{10}}{5}\) (thỏa mãn (*)). +) Nếu \(x^2+y^2< 1\Rightarrow x,y< 1\Rightarrow x+2y< 3< \frac{3+\sqrt{10}}{2}\). So sánh hai trường hợp, ta có bộ số (x, y) để x + 2y đạt max là \(x=\frac{5+\sqrt{10}}{5};y=\frac{5+2\sqrt{10}}{5}\).
L
1
AH
Akai Haruma
Giáo viên
25 tháng 1
Lời giải:
PT $\Leftrightarrow x^2-4xy+(5y^2+2y-3)=0$
Dấu "=" tồn tại nghĩa là pt luôn có nghiệm.
$\Leftrightarrow \Delta'=(2y)^2-(5y^2+2y-3)\geq 0$
$\Leftrightarrow -y^2-2y+3\geq 0$
$\Leftrihgtarrow y^2+2y-3\leq 0$
$\Leftrightarrow (y-1)(y+3)\leq 0$
$\Leftrightarrow -3\leq y\leq 1$
$\Rightarrow y_{\max}=1$
QT
1
T
27 tháng 3 2019
Biến đổi bất phương trình thành: \(\left(x^2-2xy+y^2\right)+\left(y^2-4x+4\right)+4\le0\)
\(\Leftrightarrow\left(x-y\right)^2+\left(y-2\right)^2+4\le0\) (1)
Ta có: \(\left(x-y\right)^2\ge0;\left(y-2\right)^2\ge0\)
Suy ra \(\Leftrightarrow\left(x-y\right)^2+\left(y-2\right)^2+4\ge4\) trái với (1)
Vậy không tồn x, y thỏa mãn bất pt trên.
CM
6 tháng 10 2017
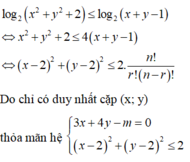
nên đường thẳng 3x + 4y - m = 0 là tiếp tuyến của đường tròn (x – 2)2 + (y – 2)2 = 2.
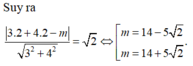
Chọn C.
BT
1
5 tháng 8 2015
x² + 5y² + 2y - 4xy - 3 = 0
<=> x² - 4xy + 4y² + y² + 2y + 1 - 4 = 0
<=> (x - 2y)² + (y + 1)² = 4 (*)
VÌ (x -2y)², (y+1)² là các số chính phương nên (*) chỉ có các khã năng:
* KN1:
{(x-2y)² = 0
{(y+1)² = 4
<=> x = 2y và y+1 = ±2 => x = 2y và y = -3 (do ta chọn y nhỏ nhất nên loại y = 1)
=> x = -6 và y = -3
* KN2:
{(x-2y)² = 4
{y+1)² = 0
<=> x - 2y = ±2 và y = -1 > -3 tức là ta chọn nghiêm y = -3 mới nhỏ nhất
Vậy cặp (x, y) cần tìm là: x = -6; y = -3
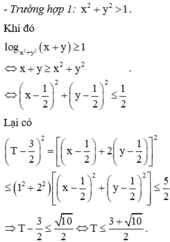
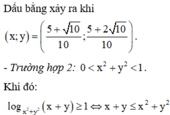
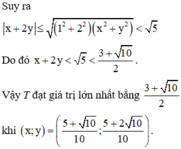
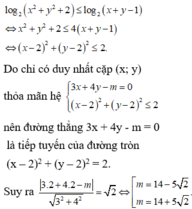
Đặt \(S=x+2y\Rightarrow x=S-2y\)
Xét 2 trường hợp :
TH1: \(x^2+y^2>1\)từ giả thiết \(\Rightarrow x^2+y^2\le x+y\Leftrightarrow\left(S-2y\right)^2+y^2\le S-y\Rightarrow5y^2-\left(4S-1\right)y+S^2-S\le0\left(1\right)\)
Coi (1) là bất pt bậc 2 đối với ẩn y
\(\Rightarrow\Delta=\left(4S-1\right)^2-20\left(S^2-S\right)\ge0\Rightarrow4S^2-12S-1\le0\Rightarrow S\le\frac{3+\sqrt{10}}{2}\)
Đẳng thức xảy ra khi \(x=\frac{5+\sqrt{10}}{2}\) thỏa mãn \(x^2+y^2>1\)
Vậy \(S_{m\text{ax}}=\frac{3+\sqrt{10}}{2}\)
TH2: Nếu \(x^2+y^2< 1\Rightarrow x+y\le x^2+y^2\)\(\Rightarrow S=x+2y\le x^2+y^2+y< 1+1=2\Rightarrow S< \frac{3+\sqrt{10}}{2}\)
Vậy S lớn nhất là \(\frac{3+\sqrt{10}}{2}\)khi \(x=\frac{5+2\sqrt{10}}{10};y=\frac{5+2\sqrt{10}}{10}\)