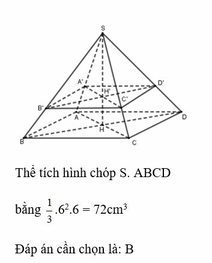
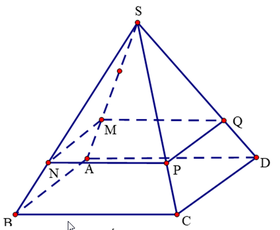
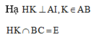Cho hình chóp tứ giác đều S.ABCD có đường cao SH = 6cm, cạnh đáy bằng 6cm. Lấy điểm H’ SH sao cho SH’ = 2 3 . Một mặt phẳng đi qua H’ và song song với đáy và cắt mặt bên của hình chóp tạo thành hình chóp nhỏ S.A’B’C’D’ và hình chóp cụt ABCD.A’B’C’D’. Tính thể tích của hình chóp S.ABCD.
A. 32 c m 3
B. 72 c m 3
C. 16 c m 3
D. 64 c m 3