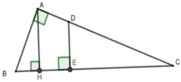
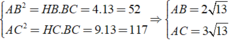
Gọi D là giao điểm của AC và đường vuông góc với BC tại E.

Xét ΔAHC và ΔABC có C chung và A H C ^ = B A C ^ = 90 ∘ nên ΔAHC ~ ΔBAC (g-g)

Ta có S D E C = 1 2 S A B C (1), S A H C : S A B C = H C B C = 9 9 + 3 , 5 = 18 25 2

Từ (1) và (2) suy ra S D E C : S A H C = 1 2 : 18 25 = 25 36 = ( 5 6 ) 2 ( 3 )

Vì DE // AH (cùng vuông với BC) duy ra ΔDEC ~ ΔAHC nên

S D E C : S A H C = ( E C H C ) 2 ( 4 )

Từ (3) và (4) suy ra E C H C = 5 6  tức là E C 9 = 5 6  => EC = 7,5cm.

Đáp án: D

Xét ΔABC có 

AD là đường phân giác ứng với cạnh BC(gt)

nên \(\dfrac{AB}{AC}=\dfrac{BD}{CD}\)(Tính chất tia phân giác của tam giác)

hay \(\dfrac{AB}{AC}=\dfrac{3}{5}\)

Ta có: \(\dfrac{AB}{AC}=\dfrac{3}{5}\)

nên \(AB=\dfrac{3}{5}AC\)

Ta có: BD+CD=BC(D nằm giữa B và C)

nên BC=36+60=96(cm)

Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow\left(\dfrac{3}{5}AC\right)^2+AC^2=96\)

\(\Leftrightarrow\dfrac{34}{25}AC^2=96\)

\(\Leftrightarrow AC^2=\dfrac{1200}{17}\)

\(\Leftrightarrow AB=\dfrac{3}{5}AC=\dfrac{3}{5}\cdot\dfrac{20\sqrt{51}}{17}=\dfrac{12\sqrt{51}}{17}\left(cm\right)\)

Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC nên 

\(\dfrac{BH}{CH}=\dfrac{AB^2}{AC^2}\)

\(\Leftrightarrow\dfrac{BH}{CH}=\dfrac{432}{17}:\dfrac{1200}{17}=\dfrac{432}{1200}=\dfrac{9}{25}\)

Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:

\(AH\cdot BC=AB\cdot AC\)

\(\Leftrightarrow AH\cdot96=\dfrac{12\sqrt{51}}{17}\cdot\dfrac{20\sqrt{51}}{17}=\dfrac{720}{17}\)

hay \(AH=\dfrac{15}{34}\left(cm\right)\)

tại sao tam giác ABC vuông tại A có AH là đg cao ứng với cạnh huyền BC thì suy ra cái kia

giải thích đc không

Áp dụng hệ thức lượng trong tam giác ABC vuông tại A

Ta có:

Vậy S A B C   =   1 2 A B . A C   =   1 2 . 2 13   . 3 13 =   39 c m 2

Chọn đáp án A.

a: Xét ΔABC vuông tại A có AH là đường cao

nên \(AH^2=HB\cdot HC\)

=>\(AH^2=1\cdot4=4\)

=>\(AH=\sqrt{4}=2\left(cm\right)\)

BC=BH+CH

=>BC=1+4=5(cm)

XétΔABC vuông tại A có AH là đường cao

nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot CB\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}AB^2=1\cdot5=5\\AC^2=4\cdot5=20\end{matrix}\right.\)

=>\(\left\{{}\begin{matrix}AB=\sqrt{5}\left(cm\right)\\AC=2\sqrt{5}\left(cm\right)\end{matrix}\right.\)

Xét ΔABC vuông tại A có \(sinC=\dfrac{AB}{BC}=\dfrac{\sqrt{5}}{5}\)

nên \(\widehat{C}\simeq27^0\)

ΔABC vuông tại A

=>\(\widehat{B}+\widehat{C}=90^0\)

=>\(\widehat{B}=90^0-27^0=63^0\)

b: AH=2cm

=>H thuộc (A;2cm)

Xét (A;2cm) có

AH là bán kính

BC\(\perp\)AH tại H

Do đó: BC là tiếp tuyến của (A;2cm)

c: Sửa đề: BDEH

Xét ΔAHB vuông tại H và ΔADE vuông tại D có

AH=AD

\(\widehat{HAB}=\widehat{DAE}\)

Do đó: ΔAHB=ΔADE

=>HB=DE

Xét tứ giác BDEH có

BH//ED

BH=ED

Do đó: BDEH là hình bình hành

1: 

Xét ΔABD và ΔACE có

AB=AC

góc B=góc C

BD=CE

=>ΔABD=ΔACE

=>AD=AE

2:

a: H là trung điểm của DB

=>D thuộc tia đối của tia HB

=>D thuộc HC

b: góc KCD=góc DAH

góc DAH=góc CED

=>góc KCD=góc CED

Xét ΔCED vuông tại E và ΔCKD vuông tại K có

CD chung

góc ECD=góc KCD

=>ΔCED=ΔCKD

=>DE=DK

a: \(AH=2\sqrt{6}\left(cm\right)\)

\(AB=2\sqrt{10}\left(cm\right)\)

\(AC=2\sqrt{15}\left(cm\right)\)

B1: Gọi Tam giác ABC vuông tại A có AH là đ/cao chia cạnh huyền thành 2 đoạn HB và HC

AH2​=HB x HC =3x4=12

AH=căn 12 r tính mấy cạnh kia đi

B2: Ta có AB/3=AC/4 suy ra AB = 3AC/4

Thế vào cong thức Pytago Tam giác ABC tính máy cái kia

Oh 2015 tuong ms dang chu :v