Giao thoa trên mặt nước hai nguồn cùng tần số, cùng pha với bước sóng 2,5cm. Khoảng cách hai nguồn S1S2 = 9cm. Có bao nhiêu gợn sống (bao gồm lồi và lõm) trong khoảng giữa S1và S2
A. 11 gợn sóng
B. 7 gợn sóng
C. 9gợn sóng
D. 5 gợn sóng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án: A
HD Giải:
Ta có: khoảng cách ngắn nhất giữa hai gợn lồi liên tiếp là 2cm → λ/2 = 2 → λ = 4cm
Hai nguồn ngược pha, nên điểm dao động với biên độ cực đại phải thỏa mãn: d2 – d1 = (k + 0,5)λ
Điểm dao động với biên độ cực tiểu thỏa mãn: d2 – d1 = k.λ
Số gợn lồi và lõm xuất hiện giữa hai điểm S1S2 là:
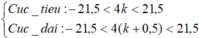
<=> 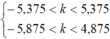
<=> 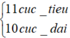

Đáp án A
Các vị trí gợn lồi gặp gợn lồi → cực đại giao thoa, ngược lại các vị trí gợn lõm gặp gợn lõm là cực tiểu giao thoa

Đáp án A
+ Các vị trí gợn lồi gặp gợn lồi → cực đại giao thoa, ngược lại các vị trí gợn lõm gặp gợn lõm là cực tiểu giao thoa

Chọn đáp án B
Hai nguồn dao động cùng pha nên ta có điểm dao động với biên độ cực đại có:
d
1
-
d
2
=
k
λ
, vân trung trực ứng với vân cực đại bậc k=0.
Tại M có
d
1
=
30
c
m
,
d
2
=
25
,
5
c
m
, tại M là một vân cực đại, giữa M và trung trực của S1S2 có thêm một gợn lồi nữa như vậy ta có M ứng với vân cực đại bậc k=2
Từ đó ta có
λ
=
2
,
25
c
m
⇒
v
=
36
c
m

Đáp án B
Phương trình dao động của hai nguồn u = A cos ω t
Phương trình dao động của điểm M thuộc CO, cách nguồn khoảng d là: u M = 2 A cos ω t − 2 π d λ
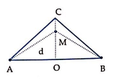
Vì điểm M dao động ngược pha với nguồn nên:
Δ φ = 2 π d λ = 2 k + 1 π ⇒ d = 2 k + 1 λ 2 = 2 k + 1 2 , 5 2 = 2 k + 1 .1 , 25
Mà A O ≤ d ≤ A C ⇒ A B 2 ≤ 2 k + 1 .1 , 25 ≤ A B 2 2 + O C 2
⇔ 12 ≤ 2 k + 1 1 , 25 ≤ 15 ⇒ 4 , 3 ≤ k ≤ 5 , 5 ⇒ k = 5
Vậy trên đoạn CO có 1 điểm dao động ngược pha với nguồn

Đáp án B
Phương trình dao động của hai nguồn ![]()
Phương trình dao động của điểm M thuộc CO, cách nguồn khoảng d là:
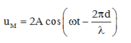
Vì điểm M dao động ngược pha với nguồn nên:
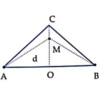
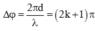
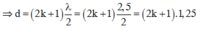
Mà ![]()
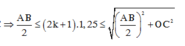
![]()
![]()
Vậy trên đoạn CO có 1 điểm dao động ngược pha với nguồn.

Khoảng cách ngắn nhất giữa hai gợn lồi liên tiếp là \(\frac{\lambda}{2} \Rightarrow \lambda = 2.2=4cm\)
Số gợn lồi (dao động cực đại) là số giá trị k thỏa mãn: \(-S_{1}S_{2}< k \lambda < S_{1}S_{2}\Rightarrow -4.125 < k < 4.125\\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3,4\)
=> có 9 gợn lồi.
Số gợn lõm (dao động cực tiểu) là số giá trị k thỏa mãn: \(-S_{1}S_{2}< (k+0.5) \lambda < S_{1}S_{2}\Rightarrow -4.125 < k+0.5 < 4.125\\ \Rightarrow -4.625 < k < 3.625 \\ \Rightarrow k = -4,-3,-2,-1,0,1,2,3.\)
=> có 8 gợn lõm.

a)Trên \(O_1O_2\) dao động cùng pha có 14 dạng hyprbol mỗi bên
\(\Rightarrow2k+1=2\cdot14+1=29\) điểm cực đại.
Khoảng cách giữa chúng:
\(l=k\cdot\dfrac{\lambda}{2}=28\cdot\dfrac{\lambda}{2}=2,8\)
\(\Rightarrow\lambda=0,2cm\)
Vận tốc truyền sóng: \(v=\lambda\cdot f=0,2\cdot100=20\)cm/s

Tham khảo:
- Cách xác định bước sóng do hai nguồn phát ra:
+ Đo khoảng cách giữa hai nguồn.
+ Đếm số khoảng cách giữa đỉnh hai gợn lồi liên tiếp hoặc số khoảng cách giữa đỉnh hai gợn lõm liên tiếp do hai nguồn tạo ra.
+ Dựa vào khái niệm bước sóng là khoảng cách gần nhau nhất giữa hai gợn lồi hoặc hai gợn lõm.
- Áp dụng:
+ Giả sử đối với hình 3.6 ở trên ta đo được khoảng cách giữa hai nguồn S1S2 = a
+ Khoảng giữa hai nguồn có 4 gợn lồi (không tính 2 nguồn) bằng 3.
Khi đó hoàn toàn tính được bước sóng \(\lambda=\dfrac{a}{3}\)
Chọn B.