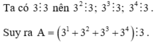
1. \(A=\frac{1}{2}-\frac{2}{5}+\frac{1}{3}+\frac{5}{7}-\frac{-1}{6}+\frac{-4}{35}+\frac{1}{41}\)

\(=\frac{1}{2}-\frac{2}{5}+\frac{1}{3}+\frac{5}{7}+\frac{1}{6}-\frac{4}{35}+\frac{1}{41}\)

\(=\left(\frac{1}{2}+\frac{1}{3}+\frac{1}{6}\right)-\left(\frac{2}{5}-\frac{5}{7}+\frac{4}{35}\right)+\frac{1}{41}\)

\(=\left(\frac{5}{6}+\frac{1}{6}\right)-\left(\frac{-11}{35}+\frac{4}{35}\right)+\frac{1}{41}\)\(=1-\frac{-7}{35}+\frac{1}{41}=1+\frac{1}{5}+\frac{1}{41}=\frac{251}{205}\)

2. a) \(1+4+4^2+4^3+......+4^{99}=\left(1+4\right)+\left(4^2+4^3\right)+.......+\left(4^{98}+4^{99}\right)\)

\(=\left(1+4\right)+4^2\left(1+4\right)+.........+4^{98}\left(1+4\right)\)

\(=5+4^2.5+........+4^{98}.5=5\left(1+4^2+.....+4^{98}\right)⋮5\)( đpcm )

b) \(3^{n+2}-2^{n+2}+3^n-2^n=\left(3^{n+2}+3^n\right)-\left(2^{n+2}+2^n\right)\)

\(=3^n\left(3^2+1\right)-2^n\left(2^2+1\right)=3^n\left(9+1\right)-2^n\left(4+1\right)\)

\(=3^n.10-2^n.5=3^n.10-2^{n-1+1}.5=3^n.10-2^{n-1}.2.5\)

\(=3^n.10-2^{n-1}.10=10\left(3^n-2^{n-1}\right)⋮10\)( đpcm )

Bài 1: 

$-1+2-3+4-5+6-7+8-...-2019+2020-2021$

$=(2+4+6+8+...+2020)-(1+3+5+...+2021)$

$=(\frac{2020-2}{2}+1).\frac{2020+2}{2}-(\frac{2021-1}{2}+1).\frac{2021+1}{2}=1021110- 1022121=-1011$

Bài 1 cách 2:

$A=-1+2-3+4-5+6-7+8-....-2019+2020-2021$

$=-1+(2-3)+(4-5)+(6-7)+....+(2020-2021)$

$=-1+\underbrace{(-1)+(-1)+...+(-1)}_{1010}=-1+(-1).1010=-1011$

Bài 1: 

Ta có: \(\left(\dfrac{1}{3}-1\right)\left(\dfrac{1}{6}-1\right)\left(\dfrac{1}{10}-1\right)\cdot...\cdot\left(\dfrac{1}{45}-1\right)\)

\(=\dfrac{-2}{3}\cdot\dfrac{-5}{6}\cdot\dfrac{-9}{10}\cdot...\cdot\dfrac{-44}{45}\)

\(=\dfrac{-2}{3}\cdot\dfrac{-5}{6}\cdot\dfrac{-9}{10}\cdot\dfrac{-14}{15}\cdot\dfrac{-20}{21}\cdot\dfrac{-27}{28}\cdot\dfrac{-35}{36}\cdot\dfrac{-44}{45}\)

\(=\dfrac{11}{27}\)

Câu 2: 

B=1+1/2+1/3+....+1/2010

 =(1+1/2010)+(1/2+1/2009)+(1/3+1/2008)+...(1/1005+1/1006)

 = 2011/2010+2011/2.2009+2011/3.2008+...+2011/1005.1006

 =2011.(1/2010+.....1/1005.1006)

Vậy B có tử số chia hết cho 2011 (đpcm).

Câu 3:

 \(P=\dfrac{2}{3}.\dfrac{4}{5}.\dfrac{6}{7}....\dfrac{98}{99}\\ P< \dfrac{3}{4}.\dfrac{5}{6}.\dfrac{6}{7}....\dfrac{99}{100}\\ P^2< \dfrac{2}{100}\)

Mà

 \(\dfrac{2}{100}=\dfrac{1}{50}< \dfrac{1}{49}\\ \Rightarrow P< \dfrac{1}{7}\)

(Mình chỉ làm đc bài 1 thôi nhé)
Bài 1:
A = 1 + 2 + 3 + 4 +...+999
2A= (1+999)+(2+998)+(3+997)+...+(999+1)
Ta nhận thấy các kết quả của các tổng trong ngoặc trên đều bằng 1000 (số chẵn), mà các số chia hết cho 2 là số chẵn, suy ra A chia hết cho 2

Cảm ơn nhee

MỌI NGƯỜI GIÚP MIK NHA!

ĐỀ ĐÂY Ạ

Bài 1:

a, 2x(3x - y)(3x+y)

= 2x(9x² - y²)

= 18x³ - 2xy²

b, (x - 5)(x + 5)

= x² - 25

Bài 2: Ta có:

(n - 1)(3 - 2n) - n(n + 5)

= 3n - 2n² - 3 + 2n - n² - 5n

= (3n + 2n - 5n) + (-2n² - n²) - 3

= -3n² - 3

= -3(n² + 1)

nên (n - 1)(3 - 2n) - n(n + 5) chia hết cho 3 với mọi n