Tìm m để hàm số y = x4 – 2mx2 + 2m + m4 – 5 đạt cực tiểu tại x = -1
A. m = -1
B. m ≠ 1
C. m = 1
D. m ≠ -1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án là B
Ta có: y ' = 4 x 3 − 4 m x , y '' = 12 x 2 − 4 m .
Hàm số đã cho đạt cực tiểu tại x = − 1 nên y ' − 1 = 0 y ' ' − 1 > 0 ⇒ − 4 + 4 m = 0 12 + 4 m > 0 ⇔ m = 1.

Đáp án C
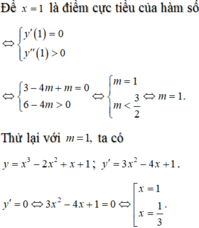
Bảng biến thiên
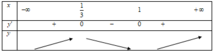
Quan sát bảng biến thiên ta thấy m=1 thỏa yêu cầu bài toán.

Ta có:
Để hàm số đã cho đạt cực tiểu tại x=1 khi và chỉ khi:
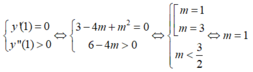
Chọn B.

Đáp án C.
Ta có y ' = 4 x 3 − 4 m + 1 x = 4 x x 2 − m − 1 .
Hàm trùng phương với hệ số a > 0 có 2 dạng:
+) Có 2 cực tiểu và 1 cực đại tại x = 0 ⇒ y ' = 0 có 3 nghiệm phân biệt.
+) có 1 cực tiểu tại x = 0 ⇒ y ' = 0 có 1 nghiệm x = 0.
Hàm số đã cho đạt cực tiểu tại x = 0 ⇔ m + 1 ≤ 0 ⇔ m ≤ − 1.

Dựa vào bảng biến thiên phần b) ta có :
C m có cực đại, cực tiểu ⇔ m > 0
Đáp án C.
Ta có y’ = 4x3 – 4mx; y’’ = 12x2 – 4m.
Để hàm số đạt cực tiểu tại x = -1 thì y’(-1) = 0 ó -4 + 4m = 0 ó m = 1
Khi m = 1 thì y’’(-1) = 12 – 4m = 12 – 4.1 = 8 > 0 => hàm số đạt cực tiểu tại x = -1.
Vậy m = 1 là giá trị cần tìm