Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
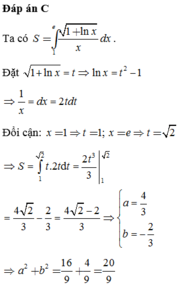
Đáp án C
Ta có S = ∫ 1 e 1 + ln x x d x . Đặt 1 + ln x = t ⇒ ln x = t 2 − 1 ⇒ 1 x = d x = 2 t d t
Đổi cận: x = 1 ⇒ t = 1 ; x = e ⇒ t = 2
⇒ S = ∫ 1 2 t .2 t d t = 2 t 3 3 2 1 = 4 2 3 − 2 3 = 4 2 − 2 3 ⇒ a = 4 3 b = − 2 3
⇒ a 2 + b 2 = 16 9 + 4 9 = 20 9
1.
\(V=\pi \int ^4_1[x^{\frac{1}{2}}e^{\frac{x}{2}}]^2dx=\pi \int ^4_1(xe^x)dx\)
\(=\pi \int ^4_1xd(e^x)=\pi (|^4_1xe^x-\int ^4_1e^xdx)\)
\(=\pi |^4_1(xe^x-e^x)=\pi (3e^4)=3\pi e^4\)
2.
\(V=\pi \int ^1_0(x\sqrt{\ln (x^3+1)})^2dx=\pi \int ^1_0x^2\ln (x^3+1)dx\)
\(=\frac{1}{3}\pi \int ^1_0\ln (x^3+1)d(x^3+1)\)
\(=\frac{1}{3}\pi \int ^2_1ln tdt=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1td(\ln t))\)
\(=\frac{1}{3}\pi (|^2_1t\ln t-\int ^2_1dt)=\frac{1}{3}\pi |^2_1(t\ln t-t)=\frac{1}{3}\pi (2\ln 2-1)\)
Chọn C.
Ta có 10 3 x - x 2 = - x ⇒ x = 0 10 3 x - x 2 = x - 2 ⇒ x = 3
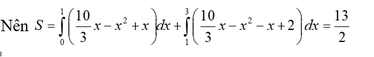
Suy ra a=13 ; b=2 và a+2b=17.
a) Diện tích hình phẳng cần tìm là:
S=2∫−1(x2+1)dx=(x33+x)∣∣2−1=6
b) Diện tích hình phẳng cần tìm là:
S=e∫1e| lnx |dx=e∫1e|lnx|dx+e∫1|lnx|dx=−1∫1elnxdx+e∫1lnxdxS=∫1ee|lnx|dx=∫1ee|lnx|dx+∫1e|lnx|dx=−∫1e1lnxdx+∫1elnxdx
Mặt khác:
∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C∫lnxdx=xlnx−∫xdlnx=xlnx−∫dx=xlnx−x+C
Do đó:
S=−1∫1elnxdx+e∫1lnxdx=1e∫1lnxdx+e∫1xdx=(xlnx−x)∣∣∣1e1+(xlnx−x)∣∣e1=2(1- \(\dfrac{1}{e}\))
Khó quá, làm mà điên não
Đáp án A
Phương trình hoành độ giao điểm e x = 2 ⇔ x = ln 2
Suy ra diện tích cần tìm bằng S = ∫ 0 ln 2 e x - 2 d x + ∫ ln 2 0 e x - 2 d x = 4 ln 2 + e - 5 .
