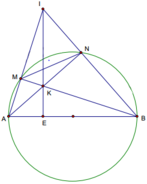
Cho nửa đường tròn đường kính AB và dây MN có độ dài bằng bán kính (M thuộc cung AN, M khác A, N khác B). Các tia AM và BN cắt nhau tại I, các dây AN và BM cắt nhau tại K.

c. Tìm vị trí của dây MN để diện tích tam giác IAB lớn nhất

cho nửa đường tròn ( o; r) đường kính ab. dây mn = r ( m thuộc cung nhỏ an) tia am cắt tia bn tại k, an cắt bm tại i. 1, cm: tứ giác kmin nội tiếp 2, cm: kn.ka=kn.kb 3. tính theo r độ dài đường thẳng ik 4 cho M , N di chuyển trên nửa đường tròn ( MN = R ) . xác định vị trí của M và N để diện tích tam giác KAB lớn nhất

Cho nửa đường tròn (O) đường kính AB và C là điểm thuộc đường tròn sao cho cung AC bằng a.Chứng minh góc CAB = 3CBA : b.Gọi M, N lần lượt là điểm chính giữa của các cung AC và BC. Hai dây AN và BM cắt nhau tại I. Chứng minh rằng tia CI là tia phân giác của ACB

Cho nửa đường tròn $(O)$ đường kính $AB$ và dây cung AC. Gọi $M$, $N$ lần lượt là các điểm chính giữa của các cung $AC$ và $BC$. Hai dây $AN$ và $BM$ cắt nhau tại $I$. Chứng minh $CI$ là tia phân giác của góc $ACB$.

Giúp em câu 3 với ạ :((
Cho nửa đường tròn (O;R) đường kính AB. Dây MN=R (M thuộc cung AN). Tia AM cắt BN tại K, AN cắt BM tại I
1. CM: KMIN là tứ giác nội tiếp
2. CM: KM.KA=KN.KB
3. Tính theo R độ dài đoạn thẳng IK

Cho nửa đường tròn (O;R), đường kính AB, dây MN =R( M thuộc cung AN), các tia AM giao BN tại I, AN giao BM tại K

a, CM I, M, K, N thuộc đường tròn.

b, CM IK vuông góc với AB

c, HA.HB=HI.HK

d, Tìm quỹ tích điểm I, điểm K khi M,N thay đổi trên đường tròn (O)

a) Cho nửa đường tròn tâm O, đường kính AB, dây CD. Các đường vuông góc với CD tại C và D tương ứng cắt AB ở M và N. Chứng minh rằng AM = BN

b) Cho nửa đường tròn tâm O, đường kính AB. Trên AB lấy các điểm M, N sao cho AM = BN. Qua M và qua N kẻ các đường thẳng song song với nhau, chúng cắt nửa đường tròn lần lượt ở C và D. Chứng minh rằng MC và ND vuông góc với CD