Cho ba điểm A, M, B phân biệt, thẳng hàng và M nằm giữa A, B. Trên cùng một nửa mặt phẳng bờ là đường thẳng AB, dựng hai tam giác đều AMC và BMD. Gọi P là giao điểm của AD và BC.
c) Đường thẳng nối tâm của hai đường tròn ngoại tiếp hai tứ giác AMPC và BMPD cắt PA, PB tương ứng tại E, F. Chứng minh CDFE là hình thang.

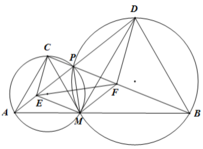
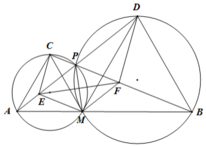

c) Ta có EF là đường trung trực của PM ⇒ EP = EM ⇒ ∆ EPM cân tại E
Mặt khác EPM = ACM = 60o (do AMPC là tứ giác nội tiếp) nên ∆ EPM đều
⇒ PE = PM . Tương tự PF = PM
Ta có CM // DB nên PCM = PBD
Mà BMPD là tứ giác nội tiếp nên PBD = PMD. Suy ra PCM = PMD
Ta lại có CPM = DPM = 120o ⇒ Δ C P M ~ Δ M P D ( g . g ) ⇒ C P M P = P M P D ⇒ C P P F = P E P D
Theo định lý Talét đảo ta có CE // DF ⇒ CDFE là hình thang.