(7x - 11) mũ 3 = 2 mũ 5 x 5 mũ 5 + 200
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


e, 2x.4 = 128
<=> 2x . 22 = 27
=> x + 2 = 7
<=> x = 5
Vậy x = 5
f , ( x - 5)4 = (x - 5)6
<=> ( x - 5)4 - (x - 5)6 =0
<=> (x - 5)4. [1 - (x - 5)2] = 0
<=> (x - 5)4 (1 - x + 5)(1 + x - 5) = 0
<=> (x - 5)4 (6 - x)(x - 4) = 0
<=> \(\left[{}\begin{matrix}x-5=0\\6-x=0\\x-4=0\end{matrix}\right.\) <=> \(\left[{}\begin{matrix}x=5\\x=6\\x=4\end{matrix}\right.\)
Vậy x ={5; 6; 4}
49 . 7x = 2041
<=> 72. 7x = 74
=> 2 + x = 4
<=> x = 2
Vậy x = 2

a, \(2^x-15=17\)
\(\Rightarrow2^x=17+15\)
\(\Rightarrow2^x=32\)
\(\Rightarrow2^x=2^5\)
\(\Rightarrow x=5\)
b, \(\left(7x-11\right)^3=2^5.5^2+200\)
\(\Rightarrow\left(7x-11\right)^3=32.25+200\)
\(\Rightarrow\left(7x-11\right)^3=1000\)
\(\Rightarrow\left(7x-11\right)^3=10^3\)
\(\Rightarrow7x-11=10\)
\(\Rightarrow7x=10+11\)
\(\Rightarrow7x=21\)
\(\Rightarrow x=21:7\)
\(\Rightarrow x=3\)
c, \(x^{10}=1^x\)
\(\Rightarrow x\in\left\{1;0\right\}\)
\(2^x-15=17\)
\(\Rightarrow2^x=17+15\)
\(\Rightarrow2^x=32=2^4\)
\(\Rightarrow x=4\)
\(\left(7x-11\right)^3=2^5.5^2+200\)
Phần này mk ko bt làm đâu
\(x^{10}=1^x\)
\(\Rightarrow\)\(x^{10}=1\)
\(\Rightarrow x=1\)

1) \(2^x-15=17\)
\(\Leftrightarrow2^x=32=2^5\)
\(\Rightarrow x=5\)
2) \(\left(7x-11\right)^3=25\cdot5^2+200\)
\(\Leftrightarrow\left(7x-11\right)^3=825\)
\(\Leftrightarrow7x-11=\sqrt[3]{825}\)
\(\Leftrightarrow7x=11+\sqrt[3]{825}\)
\(\Rightarrow x=\frac{11+\sqrt[3]{825}}{7}\)
3) \(\left(x+1\right)^{100}-3\left(x+1\right)^{99}=0\)
\(\Leftrightarrow\left(x+1\right)^{99}\left(x-2\right)=0\)
\(\Leftrightarrow\orbr{\begin{cases}\left(x+1\right)^{99}=0\\x-2=0\end{cases}}\Rightarrow\orbr{\begin{cases}x=-1\\x=2\end{cases}}\)
4) \(4x+5\left(x+3\right)=105\)
\(\Leftrightarrow9x+15=105\)
\(\Leftrightarrow9x=90\)
\(\Rightarrow x=10\)
5) \(5\cdot\left(x-2\right)+10\left(x+3\right)=170\)
\(\Leftrightarrow5\left[x-2+2\left(x+3\right)\right]=170\)
\(\Leftrightarrow3x+4=34\)
\(\Leftrightarrow3x=30\)
\(\Rightarrow x=10\)

f) \(\left(x-5\right)^4=\left(x-5\right)^6\)
\(\Rightarrow\left[{}\begin{matrix}x-5=0\\x-5=1\\x-5=-1\end{matrix}\right.\)
\(\Rightarrow\left[{}\begin{matrix}x=5\\x=6\\x=4\end{matrix}\right.\)

Bài 1:
1; 5\(x\) + \(x\) = 39 - 311 : 39
\(x\).(5 + 1) = 39 - 32
\(x.6\) = 39 - 9
\(x.6\) = 30
\(x\) = 30 : 6
\(x\) = 5
Vậy \(x\) = 5
2; 5\(x\) + \(x\) = 150 : 2 + 3
\(x\).(5 + 1) = 75 + 3
\(x.6\) = 78
\(x\) = 78 : 6
\(x\) = 13
Vậy \(x=13\)

(7*x-11)^3 = 2^5 * 5^2 +200
(7*x-11)^3 = 32*25+200
(7*x-11)^3=800+200
(7*x-11)^3=1000
=>(7*x-11)^3=(1000)^3
7*x-11=1000
7x=1000+11
7x=1011
x=1011/7
(7.x-11)^3=2^5.5^2+200
(7.x-11)^3=32.25+200
(7.x-11)^3=800+200
(7.x-11)^3=1000
(7.x-11)^3=10^3
7x-11=10
7x=10+11
7x=21
x=21/7
x=3


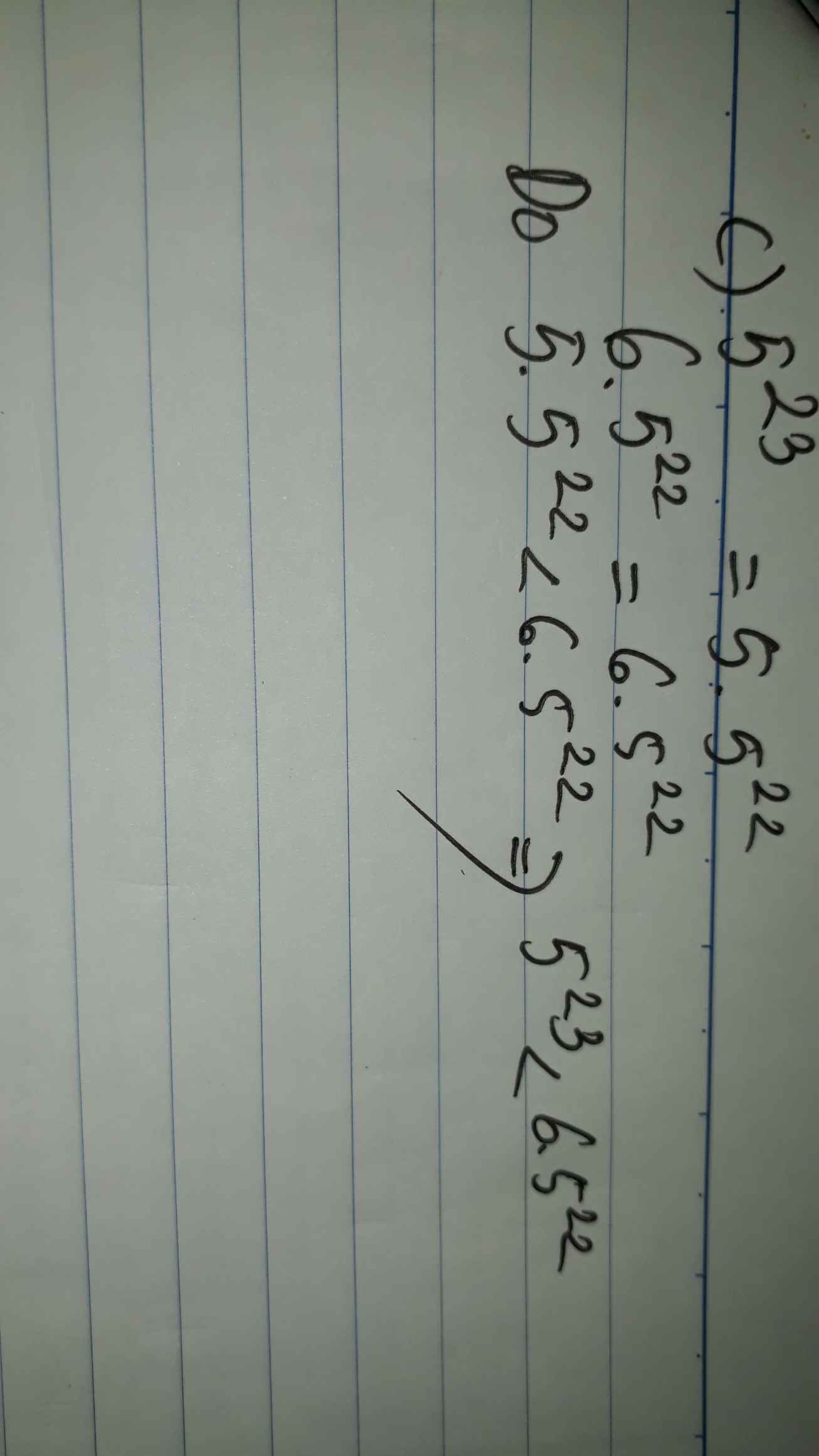
\(\Rightarrow\left(7x-11\right)^3=\left(2\cdot5\right)^5+200=10^5+200\\ \Rightarrow\left(7x-11\right)^3=10000+200=10200\\ \Rightarrow7x-11=\sqrt[3]{10200}\\ \Rightarrow x=\dfrac{\sqrt[3]{10200}+11}{7}\)