Cho các số thực dương a, b, c thỏa mãn 5 log 2 2 a + 16 log 2 2 b + 27 log 2 2 c = 1 . Giá trị lớn nhất của biểu thức S = log 2 a log 2 b + log 2 b log 2 c + log 2 c log 2 a bằng
A. 1 16
B. 1 12
C. 1 9
D. 1 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(P=loga^3+logb^2=log\left(a^3b^2\right)=log\left(100\right)=10\)

\(log_a\left(a^3b^2\right)=log_aa^3+log_ab^2=3+2\cdot log_ab\)
=>B

a) \(log_69+log_64=log_636=2\)
b) \(log_52-log_550=log_5\left(2:50\right)=-2\)
c) \(log_3\sqrt{5}-\dfrac{1}{2}log_550=-1,0479\)
Ta đi tìm GTLN của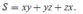
Sử dụng bất đẳng thức Cauchy – Schwarz dạng phân thức ta có
Suy ra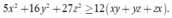
Chọn B.
Cách 2. Ghép cặp và dùng BĐT Cauchy. Cụ thể