cho hình vẽ sau , viết công thức tính độ dài các cạnh trong tam giác ABC vuông tại A, đường cao AH A B H C ...
Đọc tiếp
cho hình vẽ sau , viết công thức tính độ dài các cạnh trong tam giác ABC vuông tại A, đường cao AH
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
3 tháng 12 2021
\(a,AC=\sqrt{BC^2-AB^2}=3\sqrt{3}\left(cm\right)\\ \sin B=\dfrac{AC}{BC}=\dfrac{\sqrt{3}}{2}=\sin60^0\\ \Rightarrow\widehat{B}=60^0\\ \Rightarrow\widehat{C}=30^0\)
13 tháng 9 2016
AB=21/(3+4)x3=9 cm
AC=21-9=12cm
Tự kẻ hình bạn nhé =)))
Áp dụng định lí Pitago vào tam giác ABC , có
AB^2+AC^2=BC^2
=>thay số vào, tính được BC=15cm
Áp dụng hệ thức giữa cạnh và đường cao trong tg vuông, có:
AB^2=BHxBC
=>BH=81/15=5.4cm
=>CH=15-5.4=9.6cm
AH^2=BHxCH=5.4x9.6=51.84cm
23 tháng 2 2022
a: BC=10cm
b: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó:ΔABC\(\sim\)ΔHBA
Suy ra: AB/HB=BC/BA=AC/HA=10/6=5/3
c: AH=4,8cm
BH=3,6cm
12 tháng 1 2022
1: AC=20cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{15\cdot20}{2}=150\left(cm^2\right)\)
2: Xét tứ giác ADHE có
\(\widehat{ADH}=\widehat{AEH}=\widehat{DAE}=90^0\)
Do đó: ADHE là hình chữ nhật
3: Xét tứ giác AFDH có
AF//DH
AF=DH
Do đó: AFDH là hình bình hành
29 tháng 10 2021
b: \(AH=\dfrac{AB\cdot AC}{BC}=2.4\left(cm\right)\)
HC=3,2(cm)
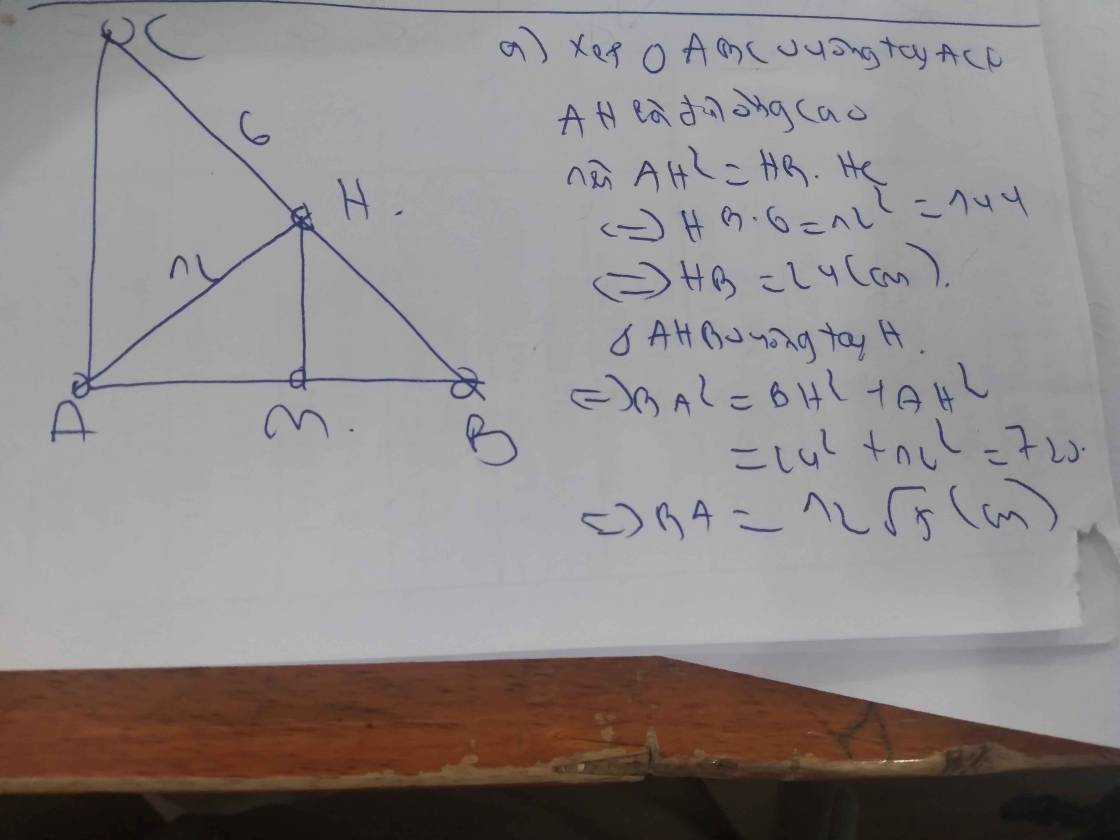
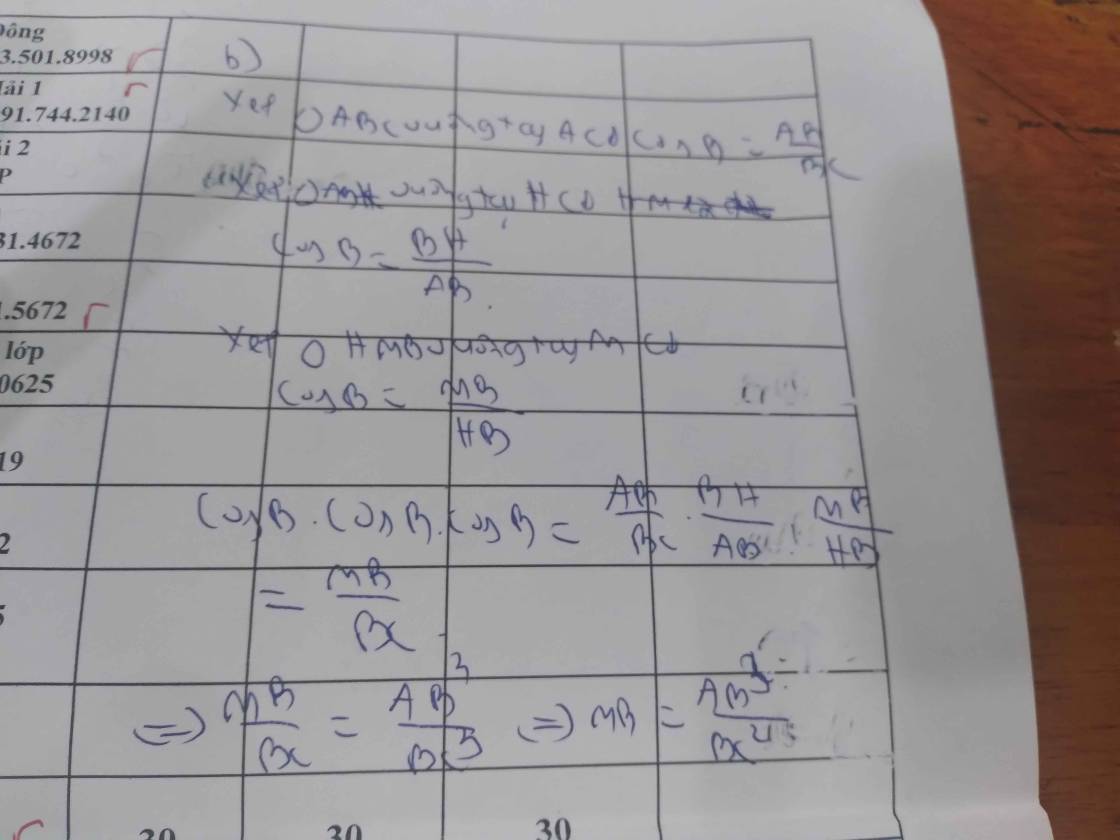
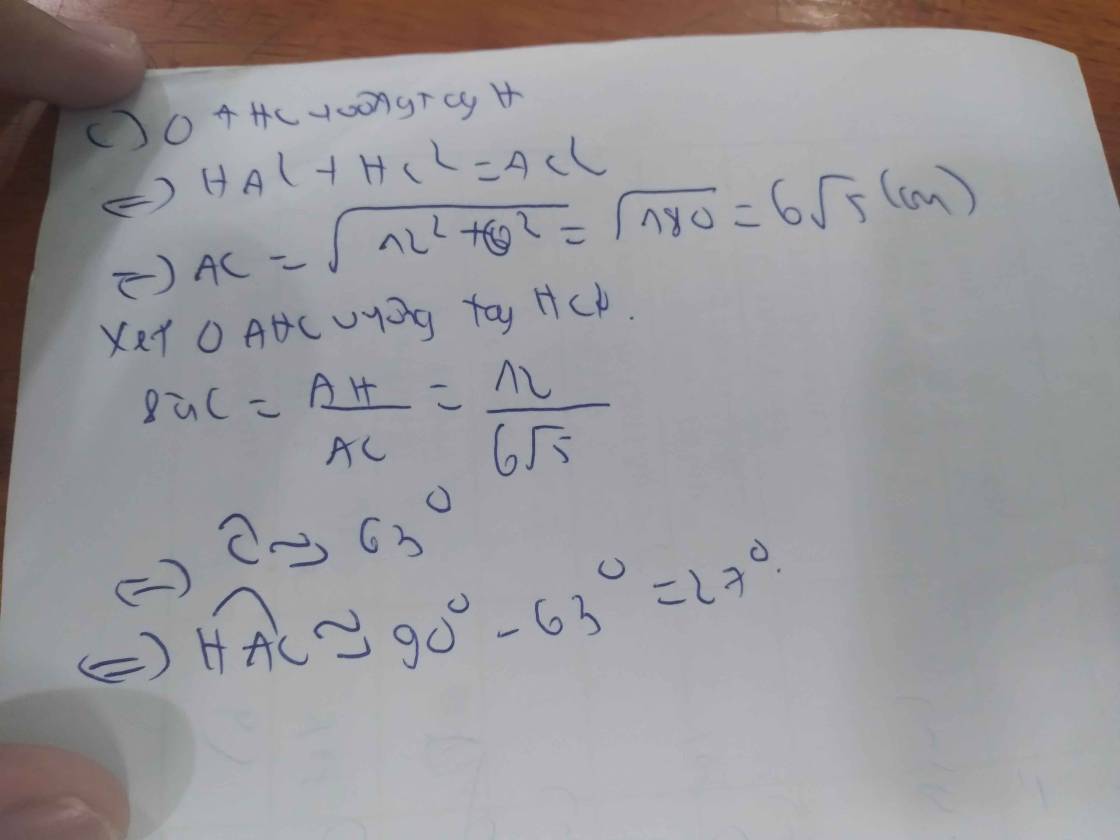
Áp dụng HTL:
\(AB^2=BH\cdot BC\\ AC^2=CH\cdot BC\\ AH^2=BH\cdot HC\\ AB\cdot AC=AH\cdot BC\\ \dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\\ AB^2+AC^2=BC^2\left(pytago\right)\)
AB2 = BC x BH
AC2 = BC x CH
AH2 = BH x CH
AH x BC = AB x AC
\(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)