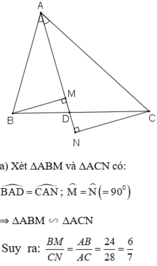
Cho tam giác ABC có các cạnh AB = 24cm, AC = 28cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M, N theo thứ tự là hình chiếu của B và C trên đường thẳng AD.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
11 tháng 10 2018
Đúng(1)
Những câu hỏi liên quan
DD
Đoàn Đức Hà
Giáo viên
11 tháng 5 2022
a) Xét tam giác \(AHD\) và tam giác \(AKD\):
\(\widehat{AHD}=\widehat{AKD}\left(=90^o\right)\)
\(AD\) cạnh chung
\(\widehat{HAD}=\widehat{KAD}\) (vì \(AD\) là tia phân giác góc \(A\) của tam giác \(ABC\))
Suy ra \(\Delta AHD=\Delta AKD\) (cạnh huyền - góc nhọn)
\(\Rightarrow AH=AK\).
b) \(\Delta AHD=\Delta AKD\) suy ra \(DH=DK\) suy ra \(D\) thuộc đường trung trực của \(HK\).
\(AH=AK\) suy ra \(A\) thuộc đường trung trực của \(HK\)
suy ra \(AD\) là đường trung trực của \(HK\).
c) Xét tam giác \(AKE\) và tam giác \(AHF\):
\(\widehat{A}\) chung
\(AH=AK\)
\(\widehat{AHF}=\widehat{AKE}\left(=90^o\right)\)
suy ra \(\Delta AKE=\Delta AHF\) (g.c.g)
suy ra \(AE=AF\)
Xét tam giác \(AEF\) có: \(\dfrac{AH}{AE}=\dfrac{AK}{AF}\) suy ra \(HK//EF\).
2 tháng 6 2020
cho tam giác abc (ab<ac) tia phân giác góc A cắt cạnh BC tại D. gọi M,N lần lượt là hình chiếu của B,C trên dường thẳng AD. chứng minh 1/dm-1/dn=2/a