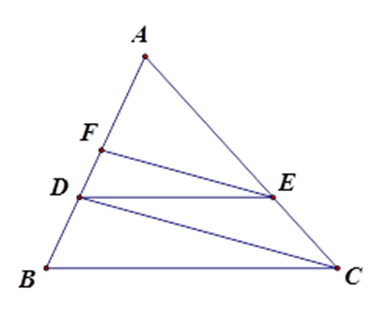
Cho tam giác ABC có AB = 9cm, điểm D thuộc cạnh AB sao cho AD = 6cm. Kẻ DE song song với BC (E Є AC), kẻ EF song song với CD (F Є AB). Tính độ dài AF.
A. 6 cm
B. 5 cm
C. 4 cm
D. 7 cm
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HQ
Hà Quang Minh
Giáo viên
13 tháng 1
Đáp án đúng là: A
Áp dụng định lí Thalès:
• Với DE // BC (E ∈ AC) ta có: \(\dfrac{{A{\rm{D}}}}{{AB}} = \dfrac{{A{\rm{E}}}}{{AC}} = \dfrac{6}{{9}} = \dfrac{2}{3}\)
• Với EF // CD (F ∈ AB) ta có: \(\dfrac{{AF}}{{A{\rm{D}}}} = \dfrac{{A{\rm{E}}}}{{AC}} = \dfrac{2}{3}\)
Suy ra: \({\rm{AF}} = \dfrac{2}{3}A{\rm{D}} = \dfrac{2}{3}.6 = 4(cm)\)
Vậy AF = 4 cm.
N
7 tháng 5 2020
Áp dụng định lí Ta-lét:
+với EF//CD ta có \(\frac{AF}{AD}=\frac{AE}{AC}\)
+với DE//BC tác có \(\frac{AE}{AC}=\frac{AD}{AB}\)
suy ra \(\frac{AF}{AD}=\frac{AD}{AB}\),
tức là \(\frac{AF}{6}\)\(=\frac{6}{9}\)
=> AF=\(\frac{6.6}{9}=4\left(cm\right)\)
CHÚC BẠN HỌC TỐT
20 tháng 12 2015
434
AI TICK GIÙM MÌNH MỘT CÁI ĐI MÀ LÀM ƠN ĐÓ!!!!!!!!!!!!!!!!!!!!!!!
6 tháng 12 2023
Xét ΔCAB và ΔCED có
\(\widehat{CAB}=\widehat{CED}\)(hai góc so le trong, DE//AB)
\(\widehat{ACB}=\widehat{ECD}\)(hai góc đối đỉnh)
Do đó: ΔCAB đồng dạng với ΔCED
=>\(\dfrac{CA}{CE}=\dfrac{AB}{ED}=\dfrac{CB}{CD}\)
=>\(\dfrac{12}{CE}=\dfrac{18}{ED}=\dfrac{9}{3}=3\)
=>\(CE=\dfrac{12}{3}=4\left(cm\right);ED=\dfrac{18}{3}=6\left(cm\right)\)
16 tháng 2 2017
Bạn ơi bạn kiểm tra lại xem có nhầm chỗ nào không vì:
Nếu EF //AD mà F,D nằm trên AB thì EF và AD có điểm F chung nên không thể //.
Áp dụng định lý Ta-lét:
Với EF // CD ta có A F A D = A E A C
Với DE // BC ta có A E A C = A D A B
Suy ra A F A D = A D A B , tức là A F 6 = 6 9
Vậy AF = 6.6 9 = 4 cm
Đáp án: C