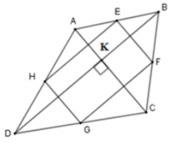
Vì E, F, G, H lần lượt là trung điểm các cạnh AB,BC,CD,DA nên EF, FG, GH, HE lần lượt là đường trung bình của tam giác ABC, BCD, ADC, ADB nên 

EF//HG (cùng song song với AC)

HE//FG (cùng song song với BD)

Suy ra tứ giác EFGH là hình bình hành

Mà  A C ⊥ B D (gt)   ⇒ E F ⊥ F G

Suy ra EFGH là hình chữ nhật

Do đó  S E F G H = H E . E F mà  E F = 1 2 A C ;  H E = 1 2 B D (tính chất đường trung bình)

a) Xét ΔABC có

E là trung điểm của AB(gt)

F là trung điểm của BC(gt)

Do đó: EF là đường trung bình của ΔABC(Định nghĩa đường trung bình của tam giác)

⇒EF//AC và \(EF=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(1)

Xét ΔADC có

H là trung điểm của AD(gt)

G là trung điểm của CD(gt)

Do đó: HG là đường trung bình của ΔADC(Định nghĩa đường trung bình của tam giác)

⇒HG//AC và \(HG=\dfrac{AC}{2}\)(Định lí 2 về đường trung bình của tam giác)(2)

Từ (1) và (2) suy ra HG//EF và HG=EF

Xét ΔABD có 

E là trung điểm của AB(gt)

H là trung điểm của AD(gt)

Do đó: EH là đường trung bình của ΔABD(Định nghĩa đường trung bình của tam giác)

⇒EH//BD và \(EH=\dfrac{BD}{2}\)(Định lí 2 về đường trung bình của tam giác)

Ta có: EH//BD(cmt)

BD⊥AC(gt)

Do đó: EH⊥AC(Định lí 2 từ vuông góc tới song song)

Ta có: HG//AC(cmt)

EH⊥AC(Cmt)

Do đó: HG⊥HE(Định lí 2 từ vuông góc tới song song)

hay \(\widehat{EHG}=90^0\)

Xét tứ giác EHGF có 

HG//EF(cmt)

HG=FE(cmt)

Do đó: EHGF là hình bình hành(Dấu hiệu nhận biết hình bình hành)

Hình bình hành EHGF có \(\widehat{EHG}=90^0\)(cmt)

nên EHGF là hình chữ nhật(Dấu hiệu nhận biết hình chữ nhật)

b) Ta có: EFGH là hình chữ nhật(cmt)

nên \(S_{EFGH}=EF\cdot EH\)

\(\Leftrightarrow S_{EFGH}=\dfrac{AC}{2}\cdot\dfrac{BD}{2}=\dfrac{10}{2}\cdot\dfrac{8}{2}=5\cdot4=20cm^2\)

Vậy: Diện tích tứ giác EFGH khi AC=10cm và BD=8cm là 20cm²

c) Hình chữ nhật EFGH trở thành hình vuông khi EH=HG

hay AC=BD

Vậy: Khi tứ giác ABCD có thêm điều kiện AC=BD thì EFGH trở thành hình vuông

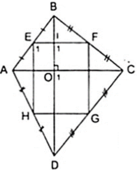
Tứ giác EFGH là hình chữ nhật.

Giải thích: Theo giả thiết ta có EF, GH lần lượt là đường trung bình của tam giác Δ ABC,Δ ADC

Áp dụng định lí đường trung bình vào hai tam giác ta được

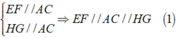
Chứng minh tương tự: EH//FG//BD      ( 2 )

Từ ( 1 ) và ( 2 ), tứ giác EFGH có hai cặp cạnh đối song song nên tứ giác EFGH là hình bình hành.

Gọi O là giao điểm của AC và BD, I là giao điểm của EF với BD.

Áp dụng tính chất của các góc đồng vị vào các đường thẳng song song ở trên và giả thiết nên ta có:

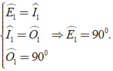
Hình bình hành EFGH có một góc vuông nên EFGH là hình chữ nhật. 

Bạn tham khảo nhé

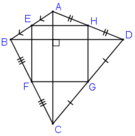
Ta có EB = EA, FB = FC (gt)

⇒ EF là đường trung bình của ΔABC

⇒EF // AC và EF = AC/2 (1)

HD = HA, GD = GC

⇒ HG là đường trung bình của ΔADC

⇒ HG // AC và HG = AC/2 (2)

Từ (1) và (2) suy ra EF // HG và EF = HG

⇒ Tứ giác EFGH là hình bình hành (*)

EA = EB, HA = HD ⇒ EH là đường trung bình của ΔABD ⇒ EH // BD.

Mà EF // AC, AC ⊥ BD

⇒ EH ⊥ EF ⇒ Ê = 90º (**)

Từ (*) và (**) suy ra EFGH là hình chữ nhật.