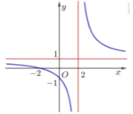
Cho hàm số y = x - a b x + c có đồ thị như hình vẽ bên. Tính giá trị của biểu thức A= a+ b+ c
A. - 2
B. -3
C. - 4
D. -5
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn D
Từ đồ thị hàm số, ta suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng x = 1, tiệm cận ngang là đường thẳng y = -1
Đồ thị hàm số đi qua các điểm A(2;0), B(0;-2)
Từ biểu thức hàm số y = a x + b x + c (vì đồ thị hàm số là đồ thị hàm nhất biến nên ac - b ≠ 0), ta suy ra
Đồ thị hàm số có tiệm cận đứng là đường thẳng x = -c, tiệm cận ngang là đường thẳng y = a.
Đồ thị hàm số đi qua ![]()
Đối chiếu lại, ta suy ra c = -1, a = -1, b
Vậy ![]()

Đáp án A
Phương pháp: Dựa vào các đường tiệm cận và các điểm đi qua của đồ thị hàm số.
Cách giải:
Đồ thị hàm số y = a x + b x + c có đường TCĐ x = – c => – c = 1 <=> c = – 1, TCN y = a => a = –1
Đồ thị hàm số đi qua (0;–1)
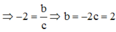
![]()

Đáp án C
Phương pháp : Xác định hàm số f’(x) từ đó tính được ![]()
Cách giải : Ta dễ dàng tìm được phương trình parabol là
![]()
![]()
Đồ thị hàm số đi qua gốc tọa độ ![]()
![]()

Ta có bảng biến thiên như hình vẽ sau:
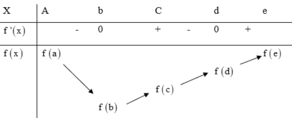
Giá trị nhỏ nhất của hàm số là f( b) nhưng giá trị lớn nhất có thể là f (a) hoặc f( e) Theo giả thiết ta có: f(a) + f( c)) = f( b) + f( d) nên f(a) - f( d)) = f( b) - f( c)< 0
Suy ra : f( a) < f( d) < f( e)
Vậy m a x [ a ; e ] f ( x ) = f ( e ) ; m i n [ a ; e ] f ( x ) = f ( b )
Chọn C.
Dựa vào đồ thị hàm số ta thấy:
Đồ thị hàm số có TCĐ và TCN là
Đồ thị hàm số đi qua điểm có tọa độ ( -2; 0) nên a= -2
Suy ra A= a+ b+ c= -2+ 1+ ( -2) = -3
Chọn B.