Cho hàm số y = f(x) = -x3 + (2m – 1)x2 – (2 – m)x – 2. Tìm m để đồ thị hàm số có cực đại và cực tiểu?
A. m ∈ (-1; +∞)
B. m ∈ (-1; 5/4)
C. m ∈ (-∞; -1)
D. m ∈ (-∞; -1) ∪ (5/4; +∞)
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có: y ' = - 3 x 2 + 2 ( 2 m - 1 ) x + m - 2 ( * )
Để hàm số đã cho có cực đại và cực tiểu khi và chỉ khi: phương trình có hai nghiệm phân biệt và y’ đổi dấu khi qua các nghiệm đó.
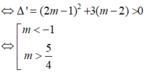
Chọn C.

Chọn D
Ta có y ' = 3 x 2 - 6 m x + m - 1
Hàm số có cực đại, cực tiểu khi và chỉ khi PT y ' = 0 có hai nghiệm phân biệt
Điều này tương đương
![]()
Hai điểm cực trị có hoành độ dương
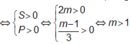
Vậy các giá trị cần tìm của m là m >1

a) y′ = 3 x 2 + 2(m + 3)x + m
y′ = 0 ⇔ 3 x 2 + 2(m + 3)x + m = 0
Hàm số đạt cực trị tại x = 1 thì:
y′(1) = 3 + 2(m + 3) + m = 3m + 9 = 0 ⇔ m = −3
Khi đó,
y′ = 3 x 2 – 3;
y′′ = 6x;
y′′(1) = 6 > 0;
Suy ra hàm số đạt cực tiểu tại x = 1 khi m = 3.
b) y′ = −( m 2 + 6m) x 2 − 4mx + 3
y′(−1) = − m 2 − 6m + 4m + 3 = (− m 2 − 2m – 1) + 4 = −(m + 1)2 + 4
Hàm số đạt cực trị tại x = -1 thì :
y′(−1) = − ( m + 1 ) 2 + 4 = 0 ⇔ ( m + 1 ) 2 = 4
⇔ 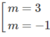
Với m = -3 ta có y’ = 9 x 2 + 12x + 3
⇒ y′′ = 18x + 12
⇒ y′′(−1) = −18 + 12 = −6 < 0
Suy ra hàm số đạt cực đại tại x = -1.
Với m = 1 ta có:
y′ = −7 x 2 − 4x + 3
⇒ y′′ = −14x − 4
⇒ y′′(−1) = 10 > 0
Suy ra hàm số đạt cực tiểu tại x = -1
Kết luận: Hàm số đã cho đạt cực đại tại x = -1 khi m = -3.

- Với \(m=0\Rightarrow y=-x^2-2\) chỉ có cực đại (thỏa mãn)
- Với \(m\ne0\) hàm chỉ có cực đại khi:
\(\left\{{}\begin{matrix}m< 0\\m\left(2m-1\right)\ge0\end{matrix}\right.\) \(\Leftrightarrow m< 0\)
Vậy \(m\le0\)

\(y'=4x^3-4mx=4x\left(x^2-m\right)\)
Hàm có cực đại, cực tiểu khi \(m>0\), khi đó ta có tọa độ các cực trị:
\(A\left(0;m^4+2m\right)\) ; \(B\left(-\sqrt{m};m^4-m^2+2m\right)\) ; \(C\left(\sqrt{m};m^4-m^2+2m\right)\)
3 cực trị luôn tạo thành 1 tam giác cân tại A
Gọi H là trung điểm BC \(\Rightarrow H\left(0;m^4-m^2+2m\right)\)
\(\Rightarrow AH=m^2\) ; \(BC=2\sqrt{m}\)
Tam giác ABC đều khi:
\(AH=\dfrac{BC\sqrt{3}}{2}\) \(\Rightarrow m^2=\sqrt{3m}\)
\(\Rightarrow m^4=3m\Rightarrow m=\sqrt[3]{3}\)

Ta có
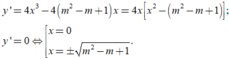
Suy ra đồ thị có hai điểm cực tiểu là A - m 2 - m + 1 ; y C T và B m 2 - m + 1 ; y C T
Khi đó 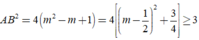
Dấu xảy ra khi m=1/2.
Chọn B.
Đáp án D.
y = -x3 + (2m – 1)x2 – (2 – m)x – 2
TXĐ: D = R
y' = -3x2 + 2(2m – 1) – 2 + m
Đồ thị hàm số có cực đại và cực tiểu <=> Pt y’ = 0 có hai nghiệm phân biệt
<=> Δ’ = (2m – 1)2 + 3(-2 + m) > 0 <=> 4m2 – m – 5 > 0 <=> m ∈ (-∞; -1) ∪ (5/4; +∞)