Cho tập A={1;2;3;4;5;6;7;8} Từ các chữ số thuộc tập A, lập được bao nhiêu số tự nhiên lẻ gồm 5 chữ số không bắt đầu bởi 123.
A.3340
B.3219
C.4942
D. 2220
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

1:{2,4};{2,3};{3,4}
2:{a,b,4},...
3:{a},....
------------------------
1 : { 2 ; 4 } ; { 2 ; 3 } ; { 3 ; 4 }
2 : { a , b , 4 } , ........
3 : { a } ,............

Từ biểu diễn của tập hợp B trên trục số, ta có điều kiện cần và đủ để A ⊂ B là
a ; a + 2 ⊂ ( − ∞ ; − 1 ) a ; a + 2 ⊂ ( 1 ; + ∞ ) ⇔ a + 2 < − 1 a > 1 ⇔ a < − 3 a > 1
Vậy tập hợp các giá trị của tham số a sao cho A ⊂ B là ( − ∞ ; − 3 ) ∪ ( 1 ; + ∞ )
Đáp án A

a, Tập hợp con của A là{1} ,{2}, A,∅
b, Để M ⊂A và M⊂B
thì M={1}
c,Vì A⊂N và B⊂N
Nên N={1;2;4}

ai bao la ko dung thi tim ra cach nhanh nhat de tinh tap con di
Xét số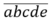 được lập từ các chữ số thuộc tập A.
được lập từ các chữ số thuộc tập A.
Vì x lẻ nên e ∈ {1; 3; 5; 7} , suy ra có 4 cách chọn e. Bốn chữ số còn lại được chọn từ 7 chữ số của tập A \ {e} nên có cách
Suy ra, có 4.840=3360 số lẻ gồm năm chữ số khác nhau.
Mà số x bắt đầu bằng 123 có số.
Vậy số x thỏa yêu cầu bài toán là :3360- 20=3340 số.
Chọn A.