Trong nhóm 60 học sinh có 30 học sinh thích học Toán, 25 học sinh thích học Lý và 10 học sinh thích cả Toán và Lý. Chọn ngẫu nhiên 1 học sinh từ nhóm này. Xác suất để được học sinh này thích học ít nhất là một môn Toán hoặc Lý?
A. 4/5
B. 3/4
C. 2/3
D. 1/2

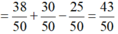

Gọi B là tập hợp “học sinh thích học Lý”
Gọi C là tập hợp ” học sinh thích học ít nhất một môn “
Ta có n(C) = n( A ∪ B) = n(A) + n(B) – n(A ∩ B) = 30 + 25 – 10 = 45
Vậy xác suất để được học sinh này thích học ít nhất là một môn Toán hoặc Lý là: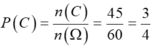
Chọn B.