Chọn C

Hướng dẫn:

Giải hệ phương trình:  k = A ' B ' A B k = − d ' d

Ta được d’ = 64 (cm)

Chọn đáp án C.

A B ¯ = 2 c m ; A ' B ' ¯ = 8 c m , d = 16 c m ; f > 0

TH1: Vật thật tạo ảnh ảo d ’   <   0 .

d > 0 ; d ' < 0 ⇒ k = − d ' d = A ' B ' ¯ A B ¯ > 0

⇒ k = − d ' d = 8 2 = 4

⇒ d ' = − 4 d = − 4.16 = − 64 ( c m )

TH2: Vật thật tạo ảnh thật d ’   >   0 .

d > 0 ; d ' > 0 ⇒ k = − d ' d = A ' B ' ¯ A B ¯ < 0

⇒ k = − d ' d = − 8 2 = − 4

⇒ d ' = 4 d = 4.16 = 64 ( c m )

Chọn đáp án D.

TH1: Vật thật tạo ảnh ảo d^’ < 0.

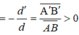
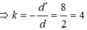
TH2: Vật thật tạo ảnh thật d^’ > 0.

Chọn đáp án C.

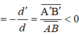
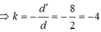
Đáp án cần chọn là: C

A B = 2 c m ;   A ’ B ’ = 8 c m ;   d = 16 c m

Ta có: k = − d ' d = A ' B ' A B = 8 2 = 4 → d ' = − 4 d = − 4.16 = − 64 c m < 0 → ảnh ảo, cách thấu kính 64cm

Đáp án C

Đáp án: C

Ảnh thật, nên

suy ra d’ = 4.d = 64cm

a. Bạn tự vẽ ( ảnh ảo )

b. Xét tam giác \(OAB\sim\) tam giác \(OA'B'\)

\(\dfrac{OA}{OA'}=\dfrac{AB}{A'B'}=\dfrac{OI}{A'B'}\)  ( do OI = AB )  (1)

Xét tam giác \(OIF'\sim\) tam giác \(A'B'F'\)

\(\dfrac{OI}{A'B'}=\dfrac{OF'}{A'F'}\) (2)

\(\left(1\right);\left(2\right)\Rightarrow\dfrac{OA}{OA'}=\dfrac{OF'}{A'F'}=\dfrac{OF'}{OA'+OF'}\)

             \(\Leftrightarrow\dfrac{8}{OA'}=\dfrac{12}{OA'+12}\)

              \(\Leftrightarrow OA'=24\left(cm\right)\)

Thế \(OA'=24\) vào \(\left(1\right)\Leftrightarrow\dfrac{1}{A'B'}=\dfrac{8}{24}\)

                                     \(\Leftrightarrow A'B'=3\left(cm\right)\)