Cho 3 lực đồng quy, đồng phẳng F → 1 , F → 2 , F → 3 lần lượt hợp với trục Ox những góc 0 0 , 60 0 , 120 0 ; F 1 = F 3 = 2 F 2 = 30 N . Tìm hợp lực của ba lực trên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Cách 1:
Lực tổng hợp của ba lực: F → = F 1 → + F 2 → + F 3 →
Tổng hợp hai lực F 1 → , F 2 → ta được F 3 →
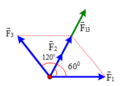
( F 1 → ; F 3 → ^ ) = 120 0 F 1 = F 3 = 10 N ⇒ F 13 = F 1 2 + F 3 2 + 2 F 1 F 3 c o s 120 0 = 10 N
Và góc giữa F 13 → với trục Ox là 600 (Δ có ba cạnhF1=F3=F13⇒Δđều)
F → = F 13 → + F 2 →
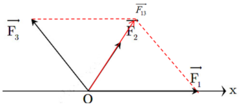
Lại có F 2 → hợp với Ox một góc 600
F 2 → ↑ ↑ F 13 → → F = F 2 + F 13 = 10 + 5 = 15 N
Cách 2:
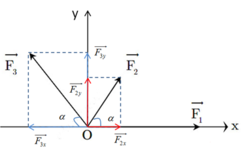
Ta có:F1=F3=2F2=10N
⇒ F 1 = 10 N F 2 = 5 N F 3 = 10 N
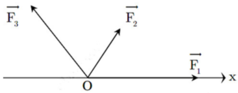
(Do đầu bài không có hình nên mình vẽ hướng của các lực như hình dưới nhé)
Phân tích các lực theo các phương Ox và Oy ta được:
F 2 x = F 2 c o s α = 5. c o s 60 0 = 2 , 5 N F 2 y = F 2 s i n α = 5. s i n 60 0 = 2 , 5 3 N
F 3 x = F 3 c o s α = 10. c o s 60 0 = 5 N F 3 y = F 3 s i n α = 10. s i n 60 0 = 5 3 N
Hợp lực theo các phương:
Phương Ox: F x → = F → 1 + F 2 x → + F 3 x →
Chiếu ta được:
F x = F 1 + F 2 x − F 3 x = 10 + 2 , 5 − 5 = 7 , 5 N
Phương Oy: F y → = F 2 y → + F 3 y →
Chiếu ta được:
F y = F 2 y + F 3 y = 2 , 5 3 + 5 3 = 7 , 5 3 N
Lực tổng hợp của 3 lực F 1 → , F 2 → , F 3 → là:
F = F x 2 + F y 2 = 7 , 5 2 + 7 , 5 3 2 = 15 N
Đáp án: A

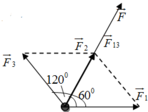
Theo bài ra ( F 1 → ; F → 3 ) = 120 0 ; F 1 = F 3 nên theo quy tắc tổng hợp hình bình hành và tính chất hình thoi ta có
( F 1 → ; F → 13 ) = 60 0 ; F 1 = F 3 = F 13 = 60 N
Mà ( F 1 → ; F → 2 ) = 60 0 ⇒ F → 2 ↑ ↑ F → 13
Vậy F = F 13 + F 2 = 60 + 60 = 120


Chọn A
Hai lực thành phần hợp nhau góc α bất kỳ thì hợp lực F tuân theo quy tắc hình bình hành
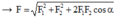

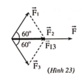
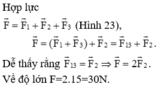
Theo bài ra ( F 1 → ; F → 3 ) = 120 0 ; F 1 = F 3 nên theo quy tắc tổng hợp hình bình hành và tính chất hình thoi
Ta có ( F 1 → ; F → 13 ) = 60 0 ; F 1 = F 3 = F 13 = 30 N
Mà ( F 1 → ; F → 2 ) = 60 0 ⇒ F → 2 ↑ ↑ F → 13
Vậy F = F 13 + F 2 = 30 + 15 = 45 N