Ba đội máy san đất làm ba khối lượng công việc như nhau. Đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai trong 6 ngày và đội thứ ba trong 8 ngày. Hỏi mỗi đội có bao nhiêu máy (có cùng năng suất) biết rằng đội thứ nhất có nhiều hơn đội thứ hai 2 máy?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số máy cày của `3` đội lần lượt là `x,y,z`\(\left(x,y,z\in N\text{*}\right)\)
Vì khối lượng và năng suất làm việc như nhau `->` Số ngày và số máy cày là `2` đại lượng tỉ lệ nghịch.
`-> 4x=4y=8z` hay ` x/(1/4)=y/(1/4)=z/(1/8)`
Đội thứ nhất nhiều hơn đội thứ `2` là `2` máy
`-> x-y=2`
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
`x/(1/4)=y/(1/4)=z/(1/8)=(x-y)/(1/4-1/4)=2/0`
`->` Đề có bị nhầm không ạ ;-;.

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{4}=\dfrac{b}{3}=\dfrac{c}{2}=\dfrac{a-b}{4-3}=2\)
Do đó: a=8; b=6; c=4

Theo bài ta có số máy và số ngày của mỗi đội là 2 đại lượng tỉ lệ nghịch nên ta có :
4.x\(_1\)=6.x\(_2\)=8.x\(_3\) và x\(_1\)-x\(_2\)=2
\(\Rightarrow\dfrac{x_1}{\dfrac{1}{4}}=\dfrac{x_2}{\dfrac{1}{6}}=\dfrac{x_3}{\dfrac{1}{8}}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\dfrac{x_1}{\dfrac{1}{4}}=\dfrac{x_2}{\dfrac{1}{6}}=\dfrac{x_3}{\dfrac{1}{8}}=\dfrac{x_1-x_2}{\dfrac{1}{4}-\dfrac{1}{6}}=\dfrac{2}{\dfrac{1}{12}}=24\)
\(\dfrac{x_1}{\dfrac{1}{4}}=24\Rightarrow x_1=24.\dfrac{1}{4}=6\)
\(\dfrac{x_2}{\dfrac{1}{6}}=24\Rightarrow x_2=24.\dfrac{1}{6}=4\)
\(\dfrac{x_3}{\dfrac{1}{8}}=24\Rightarrow x_3=24.\dfrac{1}{8}=3\)
Vậy : Đội một có 6 máy
Đội hai có 4 máy
Đội ba có 3 máy

Gọi số máy của đội thứ nhất, đội thứ hai, đội thứ ba lần lượt là a(máy),b(máy),c(máy)
(Điều kiện: \(a,b,c\in Z^+\))
Vì đội thứ nhất hoàn thành công việc trong 4 ngày, đội thứ hai hoàn thành công việc trong 6 ngày và đội thứ ba hoàn thành công việc trong 8 ngày nên ta có:
4a=6b=8c
=>\(\dfrac{4a}{24}=\dfrac{6b}{24}=\dfrac{8c}{24}\)
=>\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}\)
Ba đội có 13 máy nên a+b+c=13
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{6}=\dfrac{b}{4}=\dfrac{c}{3}=\dfrac{a+b+c}{6+4+3}=\dfrac{13}{13}=1\)
=>\(a=6\cdot1=6;b=4\cdot1=4;c=3\cdot1=3\)
Vậy: Đội thứ nhất có 6 máy
Đội thứ hai có 4 máy
Đội thứ ba có 3 máy

Gọi số máy của mỗi đội lần lượt là \(x,y,z\)(máy) \(x,y,z\inℕ^∗\)
Ta có: \(4x=6y=8z\Leftrightarrow\frac{x}{6}=\frac{y}{4}=\frac{z}{3}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\frac{x}{6}=\frac{y}{4}=\frac{z}{3}=\frac{x-y}{6-4}=\frac{2}{2}=1\)
\(\Leftrightarrow\hept{\begin{cases}x=1.6=6\\y=1.4=4\\z=1.3=3\end{cases}}\)

Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{a}{20}=\dfrac{b}{12}=\dfrac{c}{15}=\dfrac{c-b}{15-12}=1\)
Do đó: a=20; b=12; c=15
Gọi số máy của ba đội theo thứ tự là :x1,x2,x3 (máy)
Theo đề bài ta có : x1-x2=2
Vì các máy có cùng năng suất nên số máy và số ngày hoàn thành công việc là hai đại lượng tỉ lệ nghịch.
Do đó ta có :4x1 = 6x2 = 8x3 hay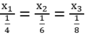
Theo tính chất của dãy tỉ số bằng nhau ta có:
Số máy của ba đội theo thứ tự là 6 ; 4 ; 3 (máy )