Một xe tải không chở hàng đang chạy trên đường. Nếu người lái xe hãm phanh thì xe trượt đi một đoạn đường s thì dừng lại. Nếu tốc độ của xe chỉ bằng một nửa lúc đầu thì đoạn đường trượt bằng bao nhiêu ?
Cho rằng lực hãm không thay đổi.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
VT
26 tháng 10 2018
Chọn chiều dương là chiều chuyển động.
Ta có v 2 - v 0 2 = 2as với v = 0 ⇒ a = - v 0 2 /2s = -F/m
Do đó s = m v 0 2 /2F
Xe chở hàng có khối lượng bằng khối lượng của xe ⇒ khối lượng tổng cộng là 2m
s 1 = 2m v 0 2 /2F = 2s
VT
20 tháng 5 2018
Vì khối lượng ô tô không đổi, lực trong hai trường hợp là như nhau nên gia tốc như nhau. Ta có:
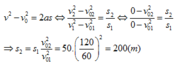
=> Chọn D
VT
12 tháng 4 2017
Chọn B.
Chọn chiều dương là chiều chuyển động. Vì lực hãm trong hai trường hợp bằng nhau nên độ lớn gia tốc bằng nhau và bằng a.
VT
29 tháng 10 2017
Đáp án D.
Do lực hãm trong hai trường hợp như nhau nên gia tốc trong hai trường hợp bằng nhau. Khi dùng lại v = 0 nên ta có:
VT
23 tháng 9 2017
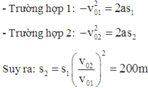
Chọn đáp án D
Đổi :
60 km/h = 50/3 m/s
120 km/h = 100/3 m/s
Lực hãm trong 2 trường hợp là như nhau
→ ôtô trong 2 trường hợp thu được gia tốc hãm là như nhau.
Áp dụng công thức:
v2 - vo2 = 2aS, khi dừng lại thì v = 0:
TH1:
02 – (50/3)2 = 2.a.50
→ a = -25/9 m/s2
TH2:
02 – (100/3)2 = 2.(-25/9).S
→ S = 200 m.
Chọn chiều dương là chiều chuyển động.
Ta có v 2 - v 0 2 = 2as với v = 0 ⇒ a = - v 0 2 /2s = -F/m
Do đó s = m v 0 2 /2F
Tốc độ của xe chỉ bằng nửa tốc độ lúc đầu v 0 /2
s 2 = m v 0 2 /(2F.4) = s/4