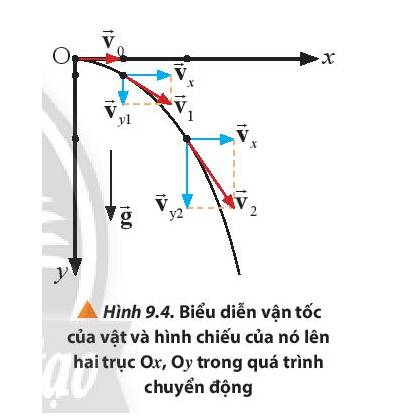
Xét chuyển động ném ngang trong mặt phẳng, vật luôn có gia tốc rơi tự do \(\overrightarrow g \) thẳng đứng hướng xuống và vuông góc với vận tốc ban đầu \(\overrightarrow {{v_0}} \)

Chọn hệ trục tọa độ Oxy như Hình 9.4, gốc thời gian là lúc thả vật

* Trên trục Ox:

- Gia tốc: a_x = 0 nên vật chuyển động thẳng đều trên Ox.

- Vận tốc: v_x = v₀ là hằng số.

- Phương trình chuyển động: x = v₀ .t.

* Trên trục Oy:

- Gia tốc: a_y = g là hằng số nên vật chuyển động nhanh dần đều trên Oy

- Vận tốc: v_y = g.t

- Phương trình chuyển động: \(y = \frac{1}{2}g{t^2}\)

Khi vật M chuyển động thì các hình chiếu Mx và My của nó trên hai trục toạ độ cũng chuyển động theo

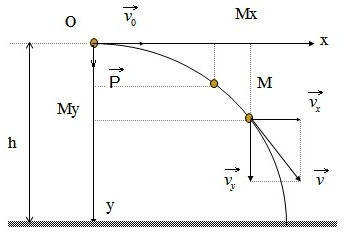
Thời gian chuyển động tổng hợp bằng thời gian chuyển động thành phần theo trục Oy. Suy ra thời gian chuyển động ném ngang của vật bằng thời gian rơi rự do từ cùng một độ cao.

\(t=\sqrt{\dfrac{2h}{y}}\)

Khi vật M chuyển động thì các hình chiếu Mx và My của nó trên hai trục toạ độ cũng chuyển động theo

Thời gian chuyển động tổng hợp bằng thời gian chuyển động thành phần theo trục Oy. Suy ra thời gian chuyển động ném ngang của vật bằng thời gian rơi rự do từ cùng một độ cao.

Những yếu tố ảnh hưởng đến tầm xa:

+ Vận tốc ném ban đầu
+ Độ cao so với mặt đất

+ Vị trí địa lí tại nơi ném (ảnh hưởng đến gia tốc trọng trường).

⇒ Cách thức tăng tầm xa khi ném ngang:

+ Tăng vận tốc ném ban đầu
+ Tăng độ cao ném so với mặt đất

Những yếu tố ảnh hưởng đến tầm xa:

+ Vận tốc ném ban đầu
+ Độ cao so với mặt đất

+ Vị trí địa lí tại nơi ném (ảnh hưởng đến gia tốc trọng trường).

=> Cách thức tăng tầm xa khi ném ngang:

+ Tăng vận tốc ném ban đầu
+ Tăng độ cao ném so với mặt đất

Chọn hệ quy chiếu gắn với mặt đất, chiều dương hướng lên, chọn mặt đất làm vật mốc

a. Ox: v_0x=v=30m/s ; a_x=0

Oy: v_0Y=0 ; a_y=-g=-10 m/s²

Ta có: x=v_0X.t=30t \(\Leftrightarrow t=\dfrac{x}{30}\)

y=\(y_0+\dfrac{1}{2}at^2\)=\(y_0-\dfrac{1}{2}gt^2\) \(=80-\dfrac{1}{2}.10.\dfrac{x^2}{30^2}\)

\(\Leftrightarrow y=80-\dfrac{1}{180}x^2\) 

Có : \(y=80-\dfrac{1}{2}.10.t^2\), thay y=0 ta được: t=4 (s)

Vậy thời gian kể từ lúc ném đến lúc chạm đất là 4(s)

c. Tầm xa của vật là: L=x=v_0X.t=30.4=120 (m)

a)Phương trình quỹ đạo: \(y=\dfrac{g}{2v_0^2}x^2=\dfrac{9,8}{2\cdot5^2}x^2=0,196x^2\)

b)Thời gian hòn đá chạm mặt nước biển: \(t=\sqrt{\dfrac{2h}{g}}=\sqrt{\dfrac{2\cdot10}{9,8}}=2,04s\)

c)Tầm xa vật: \(L=x_{max}=v_0t\)

Tọa độ Ox: \(\left\{{}\begin{matrix}v_{0x}=v_0\\a_x=0\\v_x=v_0\end{matrix}\right.\)

Tọa độ Oy: \(\left\{{}\begin{matrix}v_{0y}=0\\a_y=g\\v_y=gt\end{matrix}\right.\)

Độ lớn vận tốc: \(v=\sqrt{\left(gt\right)^2+v_0^2}\)

c)Sau 1s:

Tầm xa: \(L=v_0t=5\cdot1=5m\)

Độ lớn: \(v=\sqrt{\left(gt\right)^2+v_0^2}=\sqrt{\left(9,8\cdot1\right)^2+5^2}=11m/s\)

a)     Vận tốc ban đầu của vật v_o = v_x.

Tại thời điểm t = 2s: v_y = gt = 10.2 = 20m/s.