Xét các hình sau:
Kim tự tháp Lu-vrơ: Người ta làm mô hình một kim tự tháp ở cổng vào của bảo tàng Lu-Vrơ. Mô hình có dạng hình chóp đều cao 21m, độ dài cạnh đáy là 34m.
a. Cạnh bên hình chóp là bao nhiêu?
b. Tính thể tích hình chóp
c. Tính tổng diện tích các tẩm kính để phủ lên hình chóp này
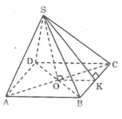


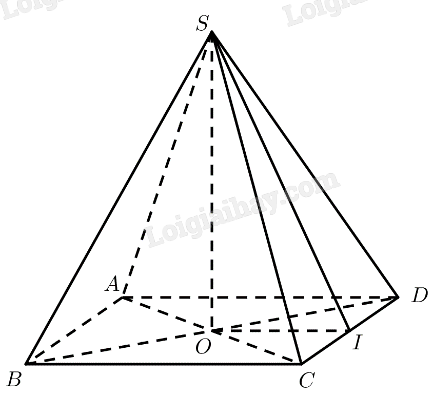



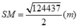
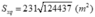
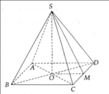
Tương tự câu 1, trong đó tổng diện tích các tấm kính để phủ lên hình chóp chính là diện tích xung quanh của hình chóp